Construction à la règle seule

Constructions interactives avec GéoPlan : uniquement à la règle non graduée, avec la règle et un cercle, avec la règle à bords parallèles.

Descartes
Faire de la géométrie dynamique

Sommaire

Si vous ne visualisez pas les figures, les contrôles ActiveX du CREEM ne sont pas installés sur votre PC. Vous pouvez voir la version non interactive de cette page : figures classiques.

Le point de concours de deux droites est situé hors de l'écran. Construire une droite passant par ce point inaccessible

Page n^o 101, créée le 4/1/2007

Construction à la règle et au compas

Constructions au compas seul

Constructions au collège

Problèmes de construction
au collège

Construction du pentagone
régulier

I.a. Construction uniquement à la règle

1. Figure constructible à la règle seule

Des points de base étant donnés, un point est constructible à la règle s'il est point d'intersection de deux droites, chacune de ces deux droites passant par deux points qui sont des points de base ou des points déjà construits.

Pour les constructions à la « règle et au compas », deux points de base suffisent.
À la règle seule, avec deux ou trois points de base il n'est pas possible d'obtenir de nouveaux points.

Construction avec quatre points de base

Première étape

On choisit quatre points A, B, C, D formant un quadrilatère autre qu'un trapèze.

On trace les six droites que ces quatre points permettent de définir.

On obtient trois nouveaux points d'intersection : E, F, G.

Deuxième étape

À partir des quatre points et des trois points d'intersection obtenus on trace les trois nouvelles droites possibles.

On obtient six nouveaux points d'intersection : H, I, J, K, L, N.

Troisième étape

Les six points H, I, J, K, L, N sont alignés, trois à trois, sur quatre droites formant un quadrilatère complet.

Et ainsi de suite…

Première étape

Télécharger la figure GéoPlan quatre_pt_base_1.g2w

Deuxième étape

Télécharger la figure GéoPlan quatre_pt_base_2.g2w

Troisième étape

Télécharger la figure GéoPlan quatre_pt_base_3.g2w

Les propriétés d'une figure constructible à la règle sont conservées par projection centrale. Ce n'est pas le cas pour les milieux, les parallèles ou les symétries.
Il en découle qu'il est impossible, avec seulement une règle, de construire le milieu d'un segment ou de mener, par un point, une parallèle à une droite.

Les figures de la géométrie projective : quadrilatère complet, polaire, théorèmes de Pappus et Desargues… sont constructibles à la règle seule ; mais pas la droite de Newton, nécessitant la notion de milieu.

2. Symétrique d'un point par rapport à une droite

On donne une droite (d), les points A et B, non situés sur (d), ainsi que le point A’ symétrique de A par rapport à (d).

Construire le point B’ symétrique de B, par rapport à (d), en utilisant la règle seule.

Solution

La droite (AB) coupe (d) en I, (A’B) en J.
Les droites (IA’) et (JA) se coupent en B’.
La droite (IA) a pour symétrique (IA’), la droite (JA’) a pour symétrique (JA).

Le point B, intersection de (IA) et (JA’) a pour symétrique l'intersection des images (IA’) et (JA), soit le point B.

Remarques : cette solution nécessite que les droites (AB) et (AB’) ne soient pas parallèles à (d).

La construction permet aussi de trouver la perpendiculaire abaissée du point B sur la droite (d) : la droite (BB’).

Télécharger la figure GéoPlan sym_point.g2w
Symétrique d'un point par rapport à une droite : voir règle à bords parallèles

3. Tracé d'une droite parallèle à deux droites (d) et (d’) parallèles

On donne deux droites parallèles distinctes (d) et (d’) et un point P.

Construire la droite parallèle à (d) et (d’) passant par le point P, en n'utilisant que la règle.

Commandes GéoPlan

Déplacer le point P,
taper 1 pour P entre les deux droites,
taper 2 pour P à l'extérieur des deux droites,
taper S pour afficher/cacher la solution.

Solution

Méthode du faisceau de droites passant par un point I, avec la polaire de P par rapport à (d) et (d’).

À partir de deux points A et B différents sur (d), tracer deux sécantes (AA’) et (BB’) passant par P avec A’ et B’ sur (d’).
Soit I le point d'intersection des droites (AB’) et (BA’).

Placer un point C, distinct de A et B, sur (d) et soit C’ l'intersection de (IC) avec (d’).
Les droites (BC’) et (CA’) se coupent en Q.

La droite (PQ) parallèle à (d) et (d’) est construite à la règle seule.

Remarques : si le point P est équidistant de (d) et (d’), les droites (AB’) et (BA’) sont parallèles et leur intersection est vide. Il faut tracer une autre parallèle : pourquoi pas la parallèle à (AB’) et (BA’) passant par C, point de (d) à l'extérieur du segment [AB]. Cette parallèle coupe (d’) en C’.
Le centre Q du parallélogramme BCC’B’ permet de trouver la parallèle (PQ).

Avec la règle à bords parallèles seule, cette méthode permet de construire la parallèle à une droite donnée passant par un point donné : en plaçant un des bords de la règle sur la droite donnée (d), le deuxième bord permet de tracer (d’). Terminer la construction de la parallèle (PQ) passant par le point donné P comme ci-dessus.

Télécharger la figure GéoPlan para_2_droites.g2w

Construction par polaires réciproques : point inaccessible
Sommaire
Faire de la géométrie dynamique

I.b. La règle et un cercle

Théorème de Poncelet-Steiner : en se donnant un cercle et son centre, avec uniquement une règle, on peut construire tout point constructible à la « règle et au compas », c'est-à-dire que l'on a la structure euclidienne.

4. Parallèle ou perpendiculaire à une droite sécante au cercle

On donne une droite (d), un point P et un cercle (c) de centre O. La droite (d), ne passe pas par le centre O et coupe le cercle en M et N.
Tracer la parallèle à (d) passant par P, ou bien la perpendiculaire, à (d) passant par P.

Solution

À l'aide des droites (OM) et (ON), on construit à la règle le rectangle MNM’N’.
Le tracé de la droite (PQ) passant par P, parallèle aux côtés parallèles du rectangle, se fait alors comme pour la règle trop courte.

Parallèle à (d) passant par P

Si le point P est équidistant de (MN) et (M’N’) la droite (PO) est parallèle à (d),

sinon il est possible de construire le point I et la droite (PQ), parallèle aux deux droites (MN) et (M’N’), est parallèle à (d).

Télécharger la figure GéoPlan para_regle.g2w

Perpendiculaire à (d) passant par P

Si le point P est équidistant de (MN’) et (NM’) la droite (PO) est perpendiculaire à (d),

sinon il est possible de construire le point I et la droite (PQ), parallèle aux deux droites (MN’) et (NM’), est perpendiculaire à (d).

Télécharger la figure GéoPlan perpen_regle.g2w

5. Perpendiculaire abaissée d'un point sur une droite passant par le centre du cercle

a. Étant donné un cercle de diamètre [AB] et un point P situé ni sur le cercle, ni sur la droite (AB), tracer, uniquement avec une règle non graduée, la perpendiculaire à (AB) issue de P.

Solution

Les droites (PA) et (PB) recoupent le cercle en R et S.
Les droites (AS) et (BR) se coupent en K.
La droite (PK) perpendiculaire à (AB) a été construite uniquement à la règle.

Démonstration

Les triangles ARB et ASB, inscrits dans les demi-cercles de diamètre [AB], sont rectangles et les angles ARK et ASP sont droits.
Le point B, intersection de deux hauteurs (KR) et (PS), est l'orthocentre du triangle APK.
Le côté (PK) est perpendiculaire à la droite (AB), troisième hauteur issue de A.

Télécharger la figure GéoPlan perpen_abaissee.g2w
Sommaire
Faire de la géométrie dynamique

b. Point P situé sur le cercle

Si le point P est situé sur le cercle, il est confondu avec R et S ne permettant pas de réaliser la construction précédente, à partir du point P.

Mais à partir d'un point K situé sur la droite (AP), distinct de P, comme ci-dessus construire une perpendiculaire intermédiaire (KL), troisième hauteur du triangle ABK d'orthocentre L. Cette perpendiculaire coupe le cercle en M et N et compléter le rectangle MNM’N’.

Si le point P est équidistant de (MN) et (M’N’) la droite (PO) est perpendiculaire à (d),
sinon (AP) et (BP) coupent (M’N’) en K’ et L’ ; le point I, intersection de (KL’) et de (LK’), permet de construire à la règle le point Q ;
la droite (PQ), parallèle aux deux droites (MN) et (M’N’), est perpendiculaire à (d).

Télécharger la figure GéoPlan perpen_regle_2.g2w

c. Repère orthonormé

Si (d) est le diamètre [II’] du cercle (c), pour construire la perpendiculaire à (d) élevée du centre O, placer un point P sur le cercle, distinct du milieu du demi-cercle II’.
Comme ci-contre, à partir d'un point K situé sur la droite (AP), construire deux droites intermédiaires (KL) et (PH), perpendiculaires à (d).

À partir des deux droites parallèles (KL) et (PH), il est possible de trouver le point I₁ intersection de (LH) et de (TL₁) permet de construire à la règle le point Q ; la droite (OQ), parallèle aux deux droites (MN) et (PH), est perpendiculaire à (d).

Cette construction fournit le point J de (c) et un repère orthonormé (O, I, J) du plan.

Télécharger la figure GéoPlan repere_regle.g2w

Voir aussi la méthode de K. Von Staudt : équation du second degré
Construire une droite passant par un point de concours situé hors de la feuille : point inaccessible
Sommaire
Faire de la géométrie dynamique

II. Règle à bords parallèles

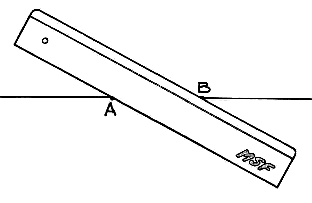Règle MSF Avec la règle à bords parallèles seule, on peut construire la parallèle à une droite donnée passant par un point donné. On a la structure affine du plan : on peut construire le milieu d'un segment.

Avec GéoPlan, nous simulerons la règle, de largeur l = 1, avec la macro « règle à bords parallèles » qui, à partir d'un des bords (d₁), tracera l'autre bord une droite (d₂) avec l'instruction :

d2 deuxième bord de la règle d1.

L'orientation induite par GéoPlan sur la droite (d₁) déterminant le côté où la règle sera tracée.

Construction de la règle passant par deux points situés sur les deux bords
Lorsque A et B sont deux points, à placer sur les bords opposés, nous tracerons le cercle de diamètre [AB] et le cercle de centre A, par exemple, et de rayon l.

Si AB ≥ l, un des points d'intersection de ces deux cercles est situé sur le bord de la règle. L'autre bord s'obtient par parallélisme.
Si AB > l, le cercle de centre B permet d'obtenir un deuxième tracé.

2.1. Configuration du losange

L'intersection de deux bandes parallèles, de même largeur, est toujours un losange.

a. Bissectrice d'un angle BÂC.

Placer la règle sur chaque côté de l'angle.
Les deux droites tracées se coupent en I formant
un losange de diagonale [AI].

(AI) est donc la bissectrice de BÂC.

Télécharger la figure GéoPlan regle_bissectrice.g2w

b. Médiatrice de [AB]

Soit [AB] un segment de longueur supérieure à la largeur de la règle.

Construction d'un losange de diagonale [AB] :
On incline la règle de telle façon que A et B soient situés chacun sur un bord de la règle. Les deux couples de parallèles ainsi créés se rencontrent en C et D. ACBD est un losange.
(CD) est la médiatrice de [AB].
[AB] coupe [CD] en son milieu (Problème 12 de l'IREM de Grenoble).

Cette figure permet aussi de trouver le milieu de [AB] intersection des deux diagonales du losange ACBD.

Télécharger la figure GéoPlan regle_losange.g2w

Sommaire
Faire de la géométrie dynamique

2.2. Partage d'un segment en parties égales

Cette méthode, plus théorique que pratique, permet de partager un segment de longueur supérieur à n fois la largeur de la règle. Dans la pratique, pour diviser le segment [AB] utiliser n règles identiques formant un réseau de droites parallèles et faire pivoter un des bords du réseau autour de A jusqu'à ce que l'autre bord rencontre B.

Avec GéoPlan, trouver B’ un des points d'intersection du cercle de diamètre [AB] et du cercle de centre A et de rayon n fois la largeur de la règle.

Le réseau de parallèles à (BB’) partage [AB].

Télécharger la figure GéoPlan regle_diviser.g2w

Lorsque le segment est trop petit, à partir d'un point A’ tracer un faisceau de n + 1 parallèles qui partage [A’B’], parallèle à [AB], en n parties égales.
Rabattre la division à partir du point O intersection de (AA’) et (BB’).

Télécharger la figure GéoPlan regle_petit_diviser.g2w

Milieu d'un segment

Avec une simple règle non graduée, sans compas on ne peut pas déterminer précisément le milieu d'un segment tracé.
Tout change si la règle est à bords parallèles.
Elle permet alors non seulement de tracer une ligne droite, mais une parallèle à cette ligne.
Comment, avec le seul soutien d'une règle non graduée à bords parallèles, est-il possible de construire le milieu d'un segment donné ?

Pour le milieu, lorsque le segment est trop court, on a la construction suivante :

Cas général - Commande GéoPlan : touche 1

– Avec la règle à bords parallèles tracer une parallèle (d) à (AB)
et placer un point C à l'extérieur de ces deux droites.
– Mener deux sécantes (CA) et (CB) qui coupent (d) en E et F.
– Tracer (BE) et (AF) qui se coupent en K.
– Le point I, intersection de (AB) et (CK), est le milieu de [AB].

Cas particulier - Collège - Commande GéoPlan : touche 2

– Avec la règle à bords parallèles tracer une parallèle (d) à (AB), et une deuxième parallèle (d₂) à (d).
– Le point C est placé sur cette deuxième parallèle.
– E et F sont alors les milieux de [AC] et [BC]. Les médianes (BE) et (AF) du triangle ABC se coupent en K son centre de gravité.
– La troisième médiane (CK) rencontre [AB] en son milieu I.

Télécharger la figure GéoPlan regle_milieu.g2w

Tiers d'un segment

À l'aide de la règle, construire un réseau de losanges identiques.

En reliant des points convenablement choisis dans ce réseau, on peut alors partager le segment [AB] en trois parties égales.

Télécharger la figure GéoPlan regle_diviser_3.g2w
Télécharger la figure Cabri regle_diviser_3.fig
Télécharger la figure GeoLabo regle_diviser_3.glb

Autres méthodes :

Partage d'un segment en trois : constructions élémentaires

Pliage d'une feuille en trois parties égales : constructions - pliages en troisième.

Sommaire
Faire de la géométrie dynamique

2.3. Parallèle à une droite

Pour tracer la parallèle à la droite (AB) passant par un point P il suffit de tracer un faisceau de trois droites parallèles à (AP) qui coupent (AB) en A, C et E.

P, A et E sont les trois premiers sommets d'un parallélogramme de centre O intersection de la deuxième parallèle et de (PE).

La droite (AO) coupe la troisième parallèle en Q, quatrième sommet du parallélogramme.

La droite (PQ) est la parallèle à (AB) cherchée.

Télécharger la figure GéoPlan regle_parallele.g2w

Sommaire
Faire de la géométrie dynamique

Voir : construction à la règle seule d'une parallèle à deux droites parallèles

2.4. Symétrique d'un point par rapport à une droite

On donne une droite (d), un point A non situé sur (d),
construire le point A’ symétrique de A par rapport à (d), en utilisant la règle à bords parallèles.

Solution

Le point A sur un des bords de la règle, on trouve les points B et C intersections des bords de la règle avec (d). On retourne la règle de telle façon que B et C soient situés chacun sur l'autre bord de la règle. On obtient un tracé symétrique des deux positions de la règle en rouge avec un losange de diagonale [BC].

On recommence avec deux autres points D et E et obtient deux autres tracés en bleu où ces deux points sont sur les bords de la règle, en traçant le losange de diagonale [DE].

A’ est le symétrique de A : c'est l'intersection des droites (BA’) et (DA’) symétriques de (BA) et (DA) par rapport à (d).

Remarque : cette construction permet aussi de trouver la perpendiculaire abaissée du point A sur la droite (d) : la droite (AH).

Télécharger la figure GéoPlan regle_sym_point.g2w
Voir aussi : symétrique d'un point par rapport à une droite
Sommaire
Faire de la géométrie dynamique

2.5. Triangle équilatéral

a. Bande de papier et son axe médian

Construction du triangle équilatéral (ou plus simplement d'un angle de 30° ou 60°)

La construction du triangle équilatéral de hauteur h se fait en plaçant un des sommets au coin d'un rectangle de largeur h. Le pied H de la hauteur [BH] est situé sur la médiatrice (A₁B₁) du rectangle. Ce point est aussi situé à une distance h de A.

Avec GéoPlan, construire le point H intersection de [A₁B₁] et du cercle de centre A passant par B. La médiatrice de [AH] coupe (AA’) en C et la droite (CH) coupe (BB’) en D qui est le troisième sommet du triangle équilatéral BCD.

Télécharger la figure GéoPlan bande_equi.g2w

Règle à bords parallèles

Sur une bande rectangulaire de largeur AB = 2l, placer A sur un bord de la règle et B sur l'autre bord, ce deuxième bord coupe le rectangle en C, reporter deux fois la règle pour obtenir le point D. BCD est équilatéral.

Télécharger la figure GéoPlan bande_equi_2.g2w

Patron du tétraèdre régulier

Pour construire un tétraèdre régulier avec cette bande, compléter la construction par quatre triangles équilatéraux.

Télécharger la figure GéoPlan bande_equi_3.g2w

b. Construction à partir de deux cercles

La règle à bords parallèles de largeur l permet de tracer un triangle équilatéral de hauteur AB = 2 l.

Avec GéoPlan, tracer deux cercles de rayon l ; l'un de diamètre [AB] et l'autre de centre A. Ces deux cercles se coupent en E et F.

AE/AB = l/2l = ; c'est le sinus de l'angle ABE = 30°. L'angle EBF vaut 60°.

Les droites (BE) et (BF) et leurs parallèles passant par A forment un losange AIBJ.

En plaçant un bord de la règle sur [IJ], l'autre passe par A ou B. Pour A on obtient la perpendiculaire à (AB) qui coupe (BE) en C et (BF) en D.

BCD, ayant (AB) comme axe de symétrie et l'angle au sommet CBD de 60°, est un triangle équilatéral.

Télécharger la figure GéoPlan regle_equilateral.g2w

La règle à bords parallèles de largeur l permet la construction complète d'un triangle équilatéral d'axe (AB’).

Première étape : construction de la médiatrice (KL) de [AB’].
Comme ci-contre. tracer le cercle de diamètre [AB’] et le cercle c₂ de centre A et de rayon l ; ces cercles se coupent en I et J. Les bords de la règle placés sur A et (BI), puis sur (BJ) forment le losange AKB’L.

Deuxième étape : construction de (AN) parallèle à (KL) passant par A.
Comme au 2.3 avec la règle tracer la troisième parallèle à (KA) et (B’L) qui coupe (KL) en M. On complète le parallélogramme de sommet A, K, M et de centre O par le point N.

Troisième étape : avec les bords de la règle construire les parallèles à (AN). Sur [AB’) on obtient les points P puis B tels que AP = l et PB = l.

Quatrième étape : terminer comme ci-contre.

Télécharger la figure GéoPlan regle_equilateral2.g2w
Voir : construction d'un triangle équilatéral par pliage d'une feuille rectangulaire
Sommaire
Faire de la géométrie dynamique

Sommaire

Faire de la géométrie dynamique

Accueil

Suggestions, remarques, problèmes : me contacter.