 Angles - TrigonométrieFigures interactives avec GéoPlan liées aux angles remarquables : 15° ; 22,5° ; 54° ; 72°. Rectangle d'or, triangle d'or. |
|
SommaireAngle 2. Angle
3. Angles a. cos |
Les pargraphes sur le nombre d'or, Les problèmes du BOA : triangle et rotation | ||||
|
Page no 35, réalisée le 17/3/2003, modifiée le 11/4/2008 | |||||
Angles | GéoPlan | GéoPlan | Construire un pentagone régulier | GéoPlan | |
1. Configuration du rectangle
|
Cliquer sur la figure, déplacer M avec la souris ou les flèches du clavier pour obtenir les valeurs approchées des
lignes trigonométriques des angles remarquables : |
Avec GéoPlan, placer un point M libre sur l'arc AB du cercle trigonométrique de centre o et de rayon 1. Utiliser les symétries {menu > point > point image par > symétrie axiale} par rapport à (Ox) puis (Oy) ou {menu > point > point image par > symétrie centrale} par rapport à O pour créer les points M1, M2, M3. Puis trouver les points H, K, H’, K’. Si ( On a : En déduire, cos(-x), sin(-x) ; cos(π - x), |
![]() Télécharger la figure GéoPlan trig_rec.g2w
Télécharger la figure GéoPlan trig_rec.g2w
Angle ![]() :
les formules de linéarisation cos2a =
:
les formules de linéarisation cos2a = 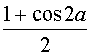 et sin2a =
et sin2a = 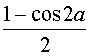 permettent de calculer les valeurs trigonométriques de l'angle moitié :
permettent de calculer les valeurs trigonométriques de l'angle moitié :
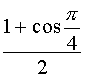 =
= 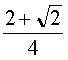 d'où cos
d'où cos![]() =
= ![]() (ce cosinus est positif)
(ce cosinus est positif)
et, de même, on trouve sin ![]() =
=
![]() .
.
Faire de la géométrie dynamique
Sommaire
2. Angle 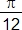
a. Calculatrice TI-92
La calculatrice formelle donne les valeurs exactes des lignes trigonométriques de ![]() :
:
cos ![]() =
= ![]() (
(![]() + 1),
sin
+ 1),
sin ![]() =
= ![]() (
(![]() - 1) et tan
- 1) et tan ![]() = 2 -
= 2 - ![]() .
.
On peut vérifier ces formules en décomposant ![]() =
=
![]() -
- ![]() :
:
Par exemple :
cos![]() = cos(
= cos(![]() -
- ![]() )
= cos
)
= cos ![]() cos
cos ![]() +
sin
+
sin ![]() sin
sin ![]() =
=
![]()
![]() +
+ ![]()
![]() =
= ![]() (
(![]() + 1)
+ 1)
Pour retrouver la tangente utiliser : 1+ tan2 x = 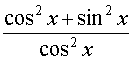 =
= 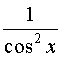 .
.
Faire de la géométrie dynamique
Sommaire
b. Triangle équilatéral dans un carré
ACDE est un carré de côté a = 2 et ABC est un triangle équilatéral.
Retrouver cette figure : angles - rotations : prouver un alignement |
Solution
- AB est égal au côté du carré, donc ABE est un triangle isocèle en A, ayant pour angle en A :
 -
-  =
= 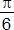 .
.
Les deux angles sont égaux à 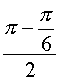 , soit
, soit ![]() ,
donc : (
,
donc : (![]() ,
, ![]() )
=
)
= ![]() -
- ![]() =
=
![]() .
.
- La hauteur du triangle équilatéral est égale à a
 =
=
 , donc BH = 2 -
, donc BH = 2 -  .
.
Dans le triangle rectangle EBH tan ![]() =
= ![]() =
= 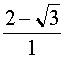 = 2 -
= 2 - ![]() ,
,
et la propriété de Pythagore donne EB2 = (2 - ![]() )2
+ 1 = 8 - 4
)2
+ 1 = 8 - 4 ![]() .
.
cos2 ![]() =
= 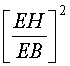 =
=
![]() =
= 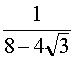 =
= 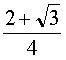
On trouve donc deux nouvelles formules : cos ![]() =
= 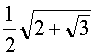 et sin
et sin ![]() =
= 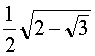 .
.
Cercle circonscrit
La médiatrice de [BE] coupe la médiatrice de [DE] en O.
Le point O est le centre du cercle circonscrit au triangle BDE,
le rayon de ce cercle est égal à la longueur du côté du carré.
![]() Télécharger la figure GéoPlan carre_t2.g2w
Télécharger la figure GéoPlan carre_t2.g2w
Faire de la géométrie dynamique
Sommaire
c. Triangle d'angles  et
et

Construire un segment AB de 5 cm. À partir du point A tracer une demi-droite formant un angle de
![]() avec (AB) et une autre à partir de B formant
un angle de
avec (AB) et une autre à partir de B formant
un angle de ![]() . Les deux demi-droites se coupent en C.
. Les deux demi-droites se coupent en C.
Soit AI, BJ et GH les trois hauteurs du triangle.
- Calculer AI, puis exprimer AC en fonction de
cos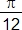 .
.
Solution
- AIB est un triangle rectangle en I. L'angle en B est par hypothèse
 ,
,
le complémentaire ( ,
,  )
=
)
= 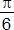 .
.
On a AI = AB cos ![]() = 5
= 5 ![]() .
.
Étudions le triangle ACI rectangle en I :
(![]() ,
, ![]() )
= (
)
= (![]() ,
, ![]() )
+ (
)
+ (![]() ,
, ![]() )
= −
)
= − ![]() +
+ ![]() =
=
![]() .
.
AI = AC cos ![]() , donc AC =
, donc AC = 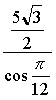 .
.
- Calculer BJ, puis exprimer BC en fonction de cos
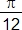 .
.
Dans le triangle ABJ rectangle en J, on a BJ = AB cos ![]() =
5
=
5 ![]() .
.
De même, dans le triangle rectangle BCJ, l'angle aigu B est égal à ![]() -
- ![]() =
= ![]() .
.
BJ = BC cos ![]() , donc BC =
, donc BC = 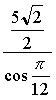 .
.
- Calcul de AC cos
 + BC cos
+ BC cos 
Dans le triangle ACH rectangle en H, d'angle A = ![]() ,
on a : AH = AC cos
,
on a : AH = AC cos ![]() .
.
Dans le triangle BCH rectangle en H, d'angle B = ![]() ,
on a : HB = BC cos
,
on a : HB = BC cos ![]() .
.
AC cos ![]() + BC cos
+ BC cos![]() =
AH + HB = AB = 5.
=
AH + HB = AB = 5.
- Calcul de cos
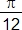
AC cos ![]() + BC cos
+ BC cos ![]() =
=
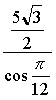
![]() +
+
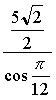
![]() =
= 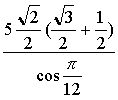 = 5.
= 5.
On retrouve la formule cos ![]() =
= ![]() (
(![]() + 1).
+ 1).
![]() Télécharger la figure GéoPlan t_pi_3_4.g2w
Télécharger la figure GéoPlan t_pi_3_4.g2w
d. Calcul de coordonnées
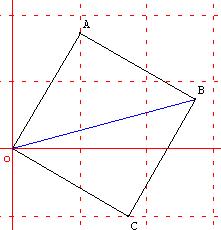 1) Le point A a pour coordonnées
polaires (2,
1) Le point A a pour coordonnées
polaires (2, ![]() ). Quelles sont ses coordonnées cartésiennes ?
). Quelles sont ses coordonnées cartésiennes ?
2) On place C image de A par la rotation r(O, - ![]() ).
).
Quelles sont les coordonnées polaires de C ?
Ses coordonnées cartésiennes ?
3) On place le point B tel que OABC soit carré : (![]() =
= ![]() +
+ ![]() ).
).
Quelle est la nature du triangle OAB ? Quel est l'angle (![]() ,
,
![]() ) ? Calculer OB.
) ? Calculer OB.
Quel est l'angle (![]() ,
, ![]() )
? Quelles sont les coordonnées polaires de B ?
)
? Quelles sont les coordonnées polaires de B ?
4) Calculer les coordonnées cartésiennes de B. En déduire les valeurs exactes de cos ![]() et sin
et sin ![]() .
.
![]() Télécharger la figure GéoPlan carre_pi_12.g2w
Télécharger la figure GéoPlan carre_pi_12.g2w
Faire de la géométrie dynamique
Sommaire
e. Complexes
Bac S Amérique du Nord 1999 - Exercice 2 - Candidats n'ayant que l'enseignement obligatoire
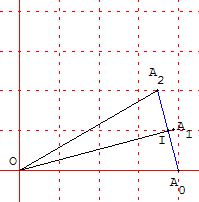 Le plan orienté est rapporté au repère orthonormal direct (O,
Le plan orienté est rapporté au repère orthonormal direct (O, ![]() ,
, ![]() ), l'unité graphique étant 4 cm. On considère les points A0, A1, d'affixes respectives : a0 = l ; a1 =
), l'unité graphique étant 4 cm. On considère les points A0, A1, d'affixes respectives : a0 = l ; a1 = ![]() .
.
Le point A2 est l'image du point A1 par la rotation r de centre O et d'angle ![]() .
.
1. a) Calculer l'affixe a2 du point A2 sous forme exponentielle puis sous forme algébrique.
b) Soit I le milieu du segment [A0A2]. Calculer l'affixe du point I.
c) Faire une figure.
2. a) Prouver que les droites (OI) et (OA1) sont confondues.
b) Écrire sous forme trigonométrique l'affixe de I.
c) Déterminer cos ![]() et sin
et sin ![]() (les valeurs exactes sont exigées), sachant que :
(les valeurs exactes sont exigées), sachant que : ![]()
![]() Télécharger la figure GéoPlan angle_pi_12.g2w
Télécharger la figure GéoPlan angle_pi_12.g2w
3. Angles 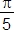 ,
, 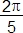
a. cos ![]() : Pour ce calcul
nous plaçons le point A sur le cercle trigonométrique tel que (
: Pour ce calcul
nous plaçons le point A sur le cercle trigonométrique tel que (![]() ,
, ![]() )
=
)
= ![]() . La rotation de centre O et d'angle
. La rotation de centre O et d'angle ![]() transforme A en B ; B en C et C en D. Les points B et C correspondent aux angles supplémentaires
transforme A en B ; B en C et C en D. Les points B et C correspondent aux angles supplémentaires ![]() et
et ![]() , B et C sont symétriques par rapport à l'axe
vertical (Oy). Le point D correspond à l'angle supplémentaire
, B et C sont symétriques par rapport à l'axe
vertical (Oy). Le point D correspond à l'angle supplémentaire ![]() ,
A et D sont symétriques par rapport à (Oy).
,
A et D sont symétriques par rapport à (Oy).
Les coordonnées de A sont :
cos ![]() = x,
= x,
sin ![]() = y.
= y.
Les formules de duplication pour l'arc double donnent :
sin 2a = 2 sin a cos a = 2 x y
cos 2a = 2 cos2a - 1 = 1 - sin2a = x2 - 1 = 1 - y2
La TI-92 calcule les fonctions trigonométriques associées au triple de l'arc (fonction dévTrig)
sin 3a = 4 sin a cos2a - sin a = 4 x2 y - y
cos 3a = cos a - 4 sin2a cos a = x - 4 x y2
B et C ont même ordonnée : sin ![]() et sin
et sin ![]() sont égaux, donc 4 x2 y - y = 2 x y.
sont égaux, donc 4 x2 y - y = 2 x y.
En simplifiant par y on obtient 4 x2 - 2 x - 1 = 0.
x = cos![]() est la solution positive de cette
équation, donc cos
est la solution positive de cette
équation, donc cos ![]() =
= ![]() ,
calcul que la TI-92 fait directement.
,
calcul que la TI-92 fait directement.
Remarque : cos![]() est égal à la moitié du nombre d'or Φ = 2 cos
est égal à la moitié du nombre d'or Φ = 2 cos![]() =
= ![]() .
.
En appliquant la formule de duplication cos2a = 2 cos2a - 1, on trouve :
cos ![]() = − cos
= − cos ![]() =
sin
=
sin ![]() = 2cos2
= 2cos2 ![]() - 1 =
- 1 = ![]() =
= 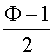 =
= ![]() .
.
x |
|
|
|
|
cos x |
|
- |
L'inverse du nombre d'or est donc ![]() = Φ
- 1 =
= Φ
- 1 = ![]() = 2 sin
= 2 sin ![]() .
.
I, B, D et les symétriques de D et B par rapport à (Ox) sont les sommets d'un pentagone régulier.
I, A, B, C, D, J et les symétriques de D, C, B et A par rapport à (Ox) sont les sommets d'un décagone régulier.
![]() Télécharger la figure GéoPlan tri_pi_5.g2w
Télécharger la figure GéoPlan tri_pi_5.g2w
Le nombre d'or
Sommaire
Faire de la géométrie dynamique
b. sin 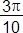
Soit D le symétrique du point A; par rapport à la droite d'équation y = x.
Le complémentaire de l'angle (![]() ,
, ![]() )
est : (
)
est : (![]() ,
, ![]() )
=
)
= ![]() .
.
OD2 = OA1 d'où sin ![]() = cos
= cos ![]() =
= ![]() .
.
Le supplémentaire de l'angle (![]() ,
, ![]() )
est : (
)
est : (![]() ,
, ![]() )
=
)
= ![]() .
.
sin![]() = sin
= sin ![]() =
=
![]() .
.
![]() Télécharger la figure GéoPlan t_pi3_10.g2w
Télécharger la figure GéoPlan t_pi3_10.g2w
Faire de la géométrie dynamique
Sommaire
c. Rectangle d'or
Un rectangle d'or est un rectangle dont le rapport de la longueur sur la largeur est égal au nombre d'or :
![]() = Φ.
= Φ.
Depuis l'antiquité grecque, on sait construire un rectangle d'or d'une largeur donnée de la façon suivante :
- tracer un carré ABCD ayant comme côté la largeur souhaitée,
- prendre le milieu K de [AD],
- rabattre le point C sur (AD) en traçant le cercle de centre K, passant par C. Ce cercle coupe [AD) en E,
- terminer la construction du rectangle d'or ABFE.
En effet, en choisissant AB = AD comme unité, on a KE = KC = ![]() d'après la propriété de Pythagore dans le triangle DKC rectangle en D,
d'après la propriété de Pythagore dans le triangle DKC rectangle en D,
et AE = ![]() +
+ ![]() = Φ.
= Φ.
![]() Télécharger la figure GéoPlan rect_or.g2w
Télécharger la figure GéoPlan rect_or.g2w
Tracé régulateur
En architecture, comme en dessin, le tracé régulateur permet de schématiser les lignes de force d'une figure.
Dans un rectangle d'or, les diagonales du rectangle rencontrent les diagonales des carrés selon des sections d'or.
Les diagonales des carrés ABCD et EFHG coupent en L, M, N, P les diagonales du rectangle d'or ABFE.
Section d'or sur une diagonale : AF/AP = AP/AM = Φ.
Section d'or sur un côté des carrés : CD/CN = CN/CP = Φ.
![]() Télécharger la figure GéoPlan rect_or4.g2w
Télécharger la figure GéoPlan rect_or4.g2w
Pavage non périodique du plan
Il est possible de paver le plan à partir de rectangles d'or. Ce pavage non régulier est formé de rectangles de plus en plus grands.
Une bonne occasion d'utiliser la fonction de création itérative de GéoPlan :
Tracer un rectangle d'or initial A0B0F0E0 à partir du carré A0B0C0D0. Tracer A0E0A1B1. B0F0A1B1 est un rectangle d'or. Remplacer A0, B0, F0, E0 respectivement par C1, F1, E1, D1 pour obtenir le rectangle d'or A1B1F1E1 contenant le carré A1B1C1D1 de niveau 1. Avec la commande d'itération (touche S) tracer les carrés suivants.
En traçant, dans chaque nouveau carré, le quart de cercle de centre Dn, reliant AnAn+1, on obtient la spirale dorée C0A0A1A2…
|
|
Cliquer sur la figure de gauche et à chaque frappe de la touche S un nouveau triangle est créé. Faire apparaître un plus grand nombre de triangles avec un zoom par appui sur la touche.
![]() Télécharger la figure GéoPlan rect_or2.g2w
Télécharger la figure GéoPlan rect_or2.g2w
Spirale logarithmique
La spirale dorée est approchée par une spirale logarithmique d'équation en coordonnées polaires
ρ = aΦ(2q/p) dans un repère d'origine I, point d'intersection de diagonales des rectangles d'or (voir figure).
Une autre spirale logarithmique passe par les sommets des rectangles d'or.
![]() Télécharger la figure GéoPlan rect_or5.g2w
Télécharger la figure GéoPlan rect_or5.g2w
voir : Robert FERRÉOL, Jacques MANDONNET : spirale d'or
Le nombre d'or
Sommaire
Faire de la géométrie dynamique
d. Triangle d'or
Le triangle d'or ACD est un triangle isocèle en C d'angle ![]() ,
les deux autres angles à la base en A et D étant égaux à
,
les deux autres angles à la base en A et D étant égaux à ![]() .
.
Le rapport entre le grand côté et la base est égal au nombre d'or : ![]() =
= ![]() = Φ.
= Φ.
Soit B le point qui partage [AC] en une section d'or :
![]() =
= ![]() = Φ,
= Φ,
on a DA = DB = BC, (DB) est la bissectrice de l'angle ![]() . Le triangle
isocèle ABD est semblable au triangle ADC avec un rapport de similitude égal à Φ. Ce triangle ABD est aussi un triangle d'or.
. Le triangle
isocèle ABD est semblable au triangle ADC avec un rapport de similitude égal à Φ. Ce triangle ABD est aussi un triangle d'or.
Cliquer sur la figure et déplacer, avec la souris, les points libres A ou C.
![]() Télécharger la figure GéoPlan trian_or.g2w
Télécharger la figure GéoPlan trian_or.g2w
Le triangle BCD est un triangle d'argent, est isocèle en B d'angle ![]() ,
les deux autres angles, en C et D, étant égaux à
,
les deux autres angles, en C et D, étant égaux à ![]() .
Le rapport des côtés est aussi égal au nombre d'or :
.
Le rapport des côtés est aussi égal au nombre d'or : ![]() = Φ.
= Φ.
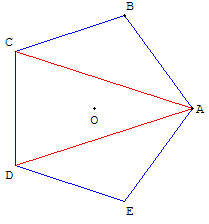 Un pentagone régulier est formé
par un triangle d'or et deux triangles d'argent.
Un pentagone régulier est formé
par un triangle d'or et deux triangles d'argent.
![]() Télécharger la figure GéoPlan pentagone.g2w
Télécharger la figure GéoPlan pentagone.g2w
Un triangle bisocèle est un triangle isocèle qui est partagé, par l'une de ses bissectrices, en deux triangles eux-mêmes isocèles.
La droite (DB), bissectrice de l'angle D du triangle ACD, partage le triangle en deux triangles isocèles. Le triangle ACD est bisocèle.
Il n'y a que deux types de triangles bisocèles : le triangle d'or et le triangle isocèle rectangle.
Voir : triangle au collège
Construction d'une section d'or
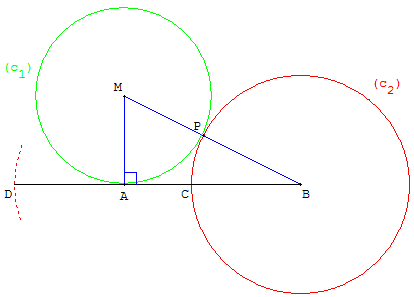 À partir du segment [AC], sur la perpendiculaire en A, placer un point M tel que AM =
À partir du segment [AC], sur la perpendiculaire en A, placer un point M tel que AM = ![]() AC.
AC.
Le cercle c1 de centre M, passant par A, coupe le segment [CM] en P.
Le cercle c2 de centre C, passant par P, coupe le segment [AC] en B qui est la section d'or cherchée.
Indications
En effet, d'après la propriété de Pythagore dans le triangle rectangle AMC, on a :
MC2 = AC2 + AM2 = (2AM)2 + AM2 = 5 AM2 d'où MC = ![]() AM.
AM.
![]() =
= ![]() =
= ![]() =
= ![]() =
= 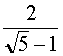 =
= ![]() = Φ.
= Φ.
![]() Télécharger la figure GéoPlan section_or.g2w
Télécharger la figure GéoPlan section_or.g2w
Construction du triangle d'or à partir du grand côté
Si A et C sont deux sommets du triangle, soit B le point qui partage [AC] en une section d'or. Le troisième sommet D est un des points d'intersection du cercle c3 de centre C, passant par A et du cercle c4 de centre B, passant par C.
Soit α = ![]() l'angle au sommet du triangle d'or. α est aussi égal à l'angle
l'angle au sommet du triangle d'or. α est aussi égal à l'angle ![]() du triangle d'or isométrique.
du triangle d'or isométrique. ![]() = 2α
car (DB) en est la bissectrice. La somme des trois angles du triangle d'or est
= 2α
car (DB) en est la bissectrice. La somme des trois angles du triangle d'or est ![]() +
+ ![]() +
+ ![]() = α + 2α + 2α = 5α = π.
= α + 2α + 2α = 5α = π.
α = ![]() . Le triangle d'or a donc un angle au sommet de
. Le triangle d'or a donc un angle au sommet de ![]() ,
les deux autres angles étant égaux à
,
les deux autres angles étant égaux à ![]() .
.
Construction d'un triangle d'or à partir de la longueur de la base
À partir du segment [AB] trouver un point C et tracer un triangle d'or ayant une base [DC] égale à AB.
On adapte ici le procédé de construction du rectangle d'or.
Soit K le milieu de [AB] et B’ le point de la perpendiculaire en B situé sur le cercle c1 de centre B, passant par A (tel que le triangle ABB’ soit rectangle isocèle direct - cf. figure).
Le cercle c2 de centre K passant par B’ coupe la demi-droite [AB) en C.
B est la section dorée de [AC].
En effet, si la longueur AB représente l'unité, la propriété de Pythagore dans le triangle rectangle KBB’ permet de vérifier que :
AC = AK + KC = AK + KB’ = ![]() +
+ ![]() = Φ.
= Φ.
Une des intersections du cercle c3 de centre A passant par C avec le premier cercle c1 de centre B est D.
ACD est un triangle d'or.
Cliquer sur la figure et déplacer, avec la souris, les points libres A ou B.
Pavage non périodique du plan
Il est possible de paver le plan à partir de triangles d'or. Ce pavage non régulier est formé de triangles de plus en plus grands.
À partir du triangle AnAn+1An+2 créer le point An+3 tel que An+1AnAn+3 soit une section d'or et recommencer.
Encore une occasion d'utiliser la fonction de création itérative de GéoPlan :
tracer un triangle d'or initial A0B0C0. Trouver le point A1 tel que B0C0A1 forme une section d'or. Remplacer A0 et B0 respectivement par B1, C1 pour obtenir le triangle d'or A1B1C1 de niveau 1. Avec la commande d'itération (touche S), tracer les triangles suivants.
|
|
|
Cliquer sur la figure de gauche et à chaque frappe de la touche S un nouveau triangle est créé. Faire apparaître un plus grand nombre de triangles avec un zoom par appui sur la touche.
![]() Télécharger la figure GéoPlan trian_or5.g2w
Télécharger la figure GéoPlan trian_or5.g2w
Spirale d'or
Une spirale logarithmique d'équation, en coordonnées polaires,
ρ = aΦ(5q/3p)
dans un repère d'origine I, intersection des droites A0A5 et A1A6 (voir figure), passe par les sommets des triangles d'or.
![]() Télécharger la figure GéoPlan tria_or6.g2w
Télécharger la figure GéoPlan tria_or6.g2w
Le nombre d'or
Construire un pentagone régulier
Le barycentre |
Angles |
GéoPlan |
GéoPlan |
GéoPlan 1S |
Démonstrations géométriques de Pythagore |
SommaireAngle 2. Angle
|
3. Angles a. cos | ||||
Faire de la géométrie dynamiqueSuggestions, remarques, problèmes : me contacter. | |||||


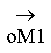 ), (
), (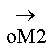 ), (
), (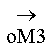 ).
).