Maximum - Minimum De nombreuses situations menant à des problèmes d'optimisation : recherche d'extrema à partir de figures géométriques	Faire de la géométrie dynamique

Technique GéoPlan : dans ces exercices est utilisée une seule figure avec deux cadres.

Commandes GéoPlan

Pour les figures interactives de cette page :

  – cliquer dans la figure,
  – taper sur la touche T pour obtenir la Trace du point variable,
  – déplacer le point variable avec les flèches du clavier (et dans certains cas avec la souris),
  – taper sur la touche S pour Sortir du mode trace et effacer la trace,
  – taper sur la touche L pour afficher ou effacer le Lieu géométrique de la trace.

1. Aire minimum de deux demi-disques

On considère la figure suivante : (C) est un cercle de centre O et de rayon 1, [AB] est un diamètre. À partir d'un point M de [AB], tracer deux demi-cercles de diamètre [AM] et [MB] (voir figure ci-dessous).
Il s'agit de trouver la position du point M où la somme des aires des demi-disques est minimum.

Indication

Le problème est posé dans le cadre géométrique. En appelant x le rayon d'un des demi-cercles, l'aire de la partie hachurée est égale à :
π (2x² - 2x + 1)/2. La résolution s'effectue dans le cadre algébrique.

Cliquer dans la figure et déplacer le point M avec les flèches du clavier.
Taper sur la touche T pour obtenir la trace du point M’,
la touche S pour Sortir du mode trace et effacer le lieu L.
Taper sur la touche L pour afficher la parabole, Lieu géométrique du point M’.

Télécharger la figure GéoPlan min_lunules.g2w

2. Aire maximum de deux lunules d'Hippocrate

Déplacer le point A et trouver la position où la somme des aires des deux lunules est maximum.

Le point M a pour coordonnées x et a_l où x est la mesure de l'angle ACB en radians et a_l l'aire des lunules.

Cliquer dans la figure et déplacer le point A avec la souris ou les flèches du clavier.
Taper sur la touche T pour obtenir la trace du point M,
taper S pour Sortir du mode trace.
Taper L pour afficher ou cacher la parabole, Lieu géométrique du point M.

Remarque : d'après le théorème des deux lunules, la somme des aires des deux lunules est égale à l'aire du triangle rectangle ABC.
On retrouve bien le fait que l'aire du triangle est maximale lorsque la hauteur issue de A est maximale. Ce maximum est atteint lorsque A est au milieu du demi-cercle de diamètre [BC], la hauteur est alors égale à BC/2, rayon du demi-cercle ; les deux lunules sont alors de même aire égale à BC²/8.

Télécharger la figure GéoPlan max_lunules.g2w
Lunules d'Hippocrate
Sommaire
Faire de la géométrie dynamique

3. Aire de l'arbelos

Arbelos d'Archimède ou tranchet du cordonnier : domaine compris entre trois demi-cercles tangents deux à deux

Cliquer dans la figure et déplacer le point M avec la souris ou les flèches du clavier.
Touche T : Tracé point par point du graphe,
touche S pour Sortir du mode trace,
touche L : dessin en bloc du graphe,
touche I : affecter la valeur 4 à x.

On considère un demi-cercle de diamètre AB = 5. M est un point (libre) du segment [AB]. On construit les demi-cercles de diamètres [AM] et [MB].

Télécharger la figure GéoPlan arbelos.g2w

Si AM = x l'aire de l'arbelos est π(5-x)x/4,
pour x = 1 ou x = 4 l'aire de l'arbelos est égale à π soit 8/25 de l'aire du demi-disque de diamètre [AB].
Pour x = 5/2, l'aire maximale est égale à la moitié de l'aire du demi-disque de diamètre [AB].

La perpendiculaire à [AB] au point M coupe le grand demi-cercle au point C.

(CM) est la hauteur, issue du sommet de l'angle droit, du triangle rectangle ABC ; MC est moyenne géométrique des projections des petits côtés sur l'hypoténuse :
MC² = AM × MB = x (5-x).
On a donc MC = , AC = et BC = .

Le cercle (c) de diamètre [CM] a la même aire que celle de l'arbelos. Il coupe les petits côtés du triangle ABC en D et E situés sur les petits demi-cercles. La droite (DE) est une tangente commune à ces demi-cercles.

Télécharger la figure GéoPlan arbelos2.g2w
Arbelos
 Glossaire publimath

Cercles d'Archimède (287-212 av. J.-C.)

en : Archimedes' circles
de : Zwillingskreise

Les cercles d'Archimède (c) et (c’) sont deux cercles inscrits dans l'arbelos, simultanément tangents à la droite (MC), au demi-cercle de diamètre [AB], au demi-cercle de diamètre [AM] pour (c) et au demi-cercle de diamètre [BM] pour (c’).

Ces deux cercles ont même diamètre d = AM × MB/AB = x (5 - x)/5.
Les centres ont pour ordonnées et .

Le cercle de diamètre [DE], tangent aux cercles (c) et (c’), a la même aire que celle de l'arbelos ; DE = CM.

Cliquer dans la figure et déplacer le point M avec la souris ou les flèches du clavier.
Touche I : affecter la valeur 4 à x.

Télécharger la figure GéoPlan arbelos3.g2w

4. Le quadrilatère qui tourne

ABCD est un rectangle de longueur a = 9 et de largeur b = 6.
À l'intérieur de ce rectangle on trace le quadrilatère MNPQ tel que AM = BN = CP = DQ = x.
Où faut-il placer M pour que l'aire du quadrilatère soit la plus petite possible ?

Première S

L'objectif de cette activité est d'introduire l'outil fonction sous sa forme algébrique : lorsque l'on déplace le point M sur [AB] étudier les variations de l'aire du parallélogramme y = A(x) de MNPQ.
Cet outil prenant du sens comme moyen de résolution d'un problème : trouver x pour que l'aire soit minimale.

Exercice sur la forme canonique de l'équation du second degré
Leçons de mathématiques à l'oral du CAPES
CRDP de Franche-Comté - 2001
Suzette Rousset-Bert - Petit x n^o 56 - IREM de Grenoble - 2001

Dans le cadre est représenté le point S(x, y)

Cliquer dans les figures et déplacer M pour trouver la position où l'aire du Parallélogramme est minimum.

Commandes :
Touche T : Tracé point par point du graphe,
touche S pour Sortir du mode trace,
touche L : dessin en bloc du graphe.

Piloter avec les flèches du clavier :
Touche A: modifier la longueur a du rectangle,
touche B: modifier la largeur b du rectangle,
touche M: déplacer le point M.

Télécharger la figure GéoPlan quadrilatere_tourne.g2w

Si a = 9 et b = 6 l'aire du quadrilatère MNPQ est égale à l'aire du rectangle ABCD moins l'aire des quatre triangles rectangles de côté x et a-x ou b-x.
L'aire du rectangle ABCD est ab = 54.
L'aire de ces quatre triangles est celle deux petits rectangles x (a-x) + x (b-x) = x (a + b - 2x) = (a + b) x - 2x² = 15 x - 2x².

On a : A(x) = 2x² - 15 x + 54
et A(x) - A(15/4) = 2(x - 15/4)².
Le minimum de l'aire est atteint pour x = 15/4 = 3,75.

Dans le cas général on a : A(x) = 2x² - (a + b) x + ab
et A(x) - A((a+b)/4) = (4x - a - b)²/8.
Le minimum de l'aire est atteint pour x = (a + b)/4.

Commandes :
Touche T : garder les Traces des points S et T,
touche S pour Sortir du mode trace,
touche L : dessin en bloc des représentations graphiques de A(x) et B(x).

Si 0 < x < b/2 ou a/2 < x < b l'aire du parallélogramme MNPQ est égale à la somme de l'aire B(x) du petit rectangle contenu dans la figure et l'aire (a + b) x - 2x² des quatre triangles rectangles. Si b/2 < x < a/2 il faut calculer la différence.

Étudier l'aire z = B(x) du petit rectangle et vérifier que le minimum de l'aire du quadrilatère est atteint lorsque le petit rectangle est un carré.

Dans le cadre sont représentés les points S(x, y) et T(x, z).

Télécharger la figure GéoPlan quadrilatere_tourne_2.g2w
Multiplication d'un parallélogramme
Sommaire
Faire de la géométrie dynamique

5. Aire et périmètre maximums d'un rectangle

AB est le « quart de cercle » situé sur le cercle de centre O et de rayon 7.

Où doit être situé le point M sur cet arc pour que l'aire du rectangle ONMP soit maximale ?

Indication

x = ON, y = OP ; OM² = ON² + OP² = x² + y² = 7² donc y² = 49 - x² soit y = .

L'aire du rectangle est xy = .

Cette aire est maximale lorsque x = 7 ≈ 4,95 (voir étude de la fonction paragraphe suivant).

Déplacer le point M sur l'arc de cercle et trouver sa position pour que l'aire du rectangle ONMP soit maximale.

Lorsque le point M est variable sur le segment [AB], on trouve une parabole : voir analyse en 1L.

Télécharger la figure GéoPlan max_rectangle.g2w

Classe de seconde

Où doit être situé le point M sur cet arc pour que le périmètre du rectangle ONMP soit maximal ?

Déplacer le point M sur l'arc de cercle et trouver sa position pour que périmètre du rectangle ONMP soit maximal.

Télécharger la figure GéoPlan max_rectangle_peri.g2w
Sommaire
Faire de la géométrie dynamique

Variante

ÉduSCOL - Terminale S - Banque de sujets 2005 - Sujet 30

Soit C un cercle de rayon 4 cm.
Quelle est l'aire maximale d'un rectangle dont les sommets sont sur le cercle.

6. Aire maximum d'un triangle

Peut-on construire un triangle isocèle d'aire maximum ?

Le triangle ABC, isocèle de sommet A est tel que c = AC = BC (c est initialisé à 7).

Le point A est libre ; x la demi-base , y est l'aire A(x) du triangle ABC. Dans le cadre est représenté le point S(x, y).

Utilisation du logiciel GéoPlan

L'intérêt est de visualiser comment l'aire du triangle varie en fonction de la longueur de la base.

Commandes GéoPlan :

Le déplacement de A se fait au clavier ou à la souris,
touche T : lieu du point S
touche L : faire apparaître ou disparaître le lieu de S.
touche C : modifier c, longueur des côtés BC et BC, au clavier.

Solution

L'aire A(x) du triangle ABC, demi-produit de la base AB par la hauteur AH, est donnée par la fonction :

A(x) = = ,   x Î [0, 10].

L'aire du triangle est aussi égale à = .

Cette aire est maximale lorsque sin C est maximal, c'est-à-dire lorsque l'angle ACB est droit.

Le maximum correspond à un triangle rectangle isocèle. L'hypoténuse 2x est alors égale c, soit x = c.

Télécharger la figure GéoPlan max_aire_triangle.g2w

7. Aire et périmètre maximums, d'un triangle inscrit dans un cercle

Le triangle ABC, isocèle de sommet A est inscrit dans un cercle (c) donné de centre O et de rayon 1.

Trouver le triangle ayant l'aire maximale.

H est un point libre du diamètre [AJ] du cercle (c). La perpendiculaire en H à (AO) coupe le cercle en B et C. Le triangle isocèle ABC est inscrit dans le cercle (c).

Soit x = AH, la longueur de la hauteur en A du triangle ABC, variant de 0 à 2. L'aire y du triangle ABC est représentée dans le cadre de droite par le point S(x, y).

En déplaçant le point H, on peut conjecturer que l'aire est maximale pour x = et ABC est un triangle équilatéral.

Commandes GéoPlan

Le déplacement de H se fait au clavier ou à la souris,
touche T pour la trace de S, touche S pour Sortir du mode trace,
la touche L fait apparaître ou disparaître le lieu de S.

Télécharger la figure GéoPlan max_triangle.g2w

Variante

Épreuve pratique 2007 - Terminale S - Sujet 027

On considère un triangle ABC isocèle en A, de périmètre fixé. Il s'agit de déterminer parmi tous les triangles possibles celui dont l'aire est maximale.

Trouver le triangle ayant le périmètre maximal.

Soit x = AH et y représente dans cette deuxième figure le périmètre de ABC. Dans le cadre de droite est représenté le point P(x, y).

En déplaçant le point H, on peut conjecturer que le périmètre est maximal pour la même valeur x = .

Télécharger la figure GéoPlan max_triangle1.g2w

Indications

Le cercle (c) ensemble des points B tels que BO² = (x - 1)² + y² = 1 a pour équation x² + y² - 2x = 0 dans un repère d'origine A.
D'où BH = . L'aire du triangle est A(x) = x.
Montrer que A() est le maximum revient à démontrer que x²(2x - x²) ≤ , soit 16x⁴ - 32x³ + 27 ≥ 0.

16x⁴ - 32x³ + 27 = (2x - 3)² (4x² + 4x + 3) est positif pour x appartenant à [0, 2].

Utilisation du logiciel GéoPlan

Sur une même figure, dans le cadre de droite sont représentés simultanément les points S(x, y) et P(x, z) où y est l'aire du triangle ABC et z est le périmètre de ABC. L'intérêt est de suivre simultanément les positions correspondantes de S et P et de montrer que le maximum de chaque fonction est atteint pour la même valeur de x.

Télécharger la figure GéoPlan max_triangle2.g2w

Il est aussi possible d'étudier les variations en fonction de x = BC : télécharger la figure GéoPlan max_triangle3.g2w

Sommaire
Faire de la géométrie dynamique

8. Fonction définie par une aire

B. Destainville
Des activités pour les classes de première
Publication APMEP n^o 85 - 1991

Énoncé (Première S)

Dans la figure ci-dessous AB = 8, AI = 2. [Ax) et [Bx’)sont deux demi-droites perpendiculaires à [AB]. M est un point variable sur [Ax) et N est le point de [Bx’) tel que le triangle MIN soit rectangle en I.

Soit x = AM et y = A(x) l'aire du triangle.

Résolution du problème

On se propose de faire une étude algébrique du comportement de A(x) lorsque M décrit [Ax).
Montrer que les côtés des triangles MAI et IBN sont proportionnels.
En déduire que A(x) = et étudier la fonction.

Commandes GéoPlan:

T : laisse la Trace du point S
S : Sortir du mode trace
L : Lieu du point S

Télécharger la figure GéoPlan fct_aire_triangle.g2w
Sommaire
Faire de la géométrie dynamique

9. Deux cercles tangents, tangents à un carré - Olympiades Poitiers 2002

Les olympiades académiques
Brochure APMEP n^o 146 - 2002

Énoncé

Soit un carré ABCD de côté a. Un cercle (c) intérieur au carré est tangent à (AB) et (AD). Un cercle (c’), intérieur au carré est tangent extérieurement à (c) ainsi qu'aux droites (CB) et (CD).

Soit S la somme des aires des cercles (c) et (c’). Quelles sont les valeurs maximales et minimales de S ?

Indication

Les centres O et O’ des cercles étant à égale distance des côtés, ils sont situés sur la diagonale [AC] du carré.
Les rayons r et r’ des cercles vérifient :

OA + r + r’ + O’C = AC = a
(r + r’) (1 + ) = a

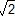
C'est-à-dire : r + r’ = a (2 - )

Les cercles étant situés à l'intérieur d'un carré de côté a, leurs rayons restent inférieurs à .
On en déduit que chaque rayon appartient à l'intervalle .

La somme des aires des deux cercles est :

S = π(r² + r’²) = [(r + r’)² - (r - r’)²] = [(6 - 4)a² - (r - r’)²]

On en déduit immédiatement que cette aire est minimale quand r = r’ = et vaut alors S_min = π(3 - 2 )a².

Et l'aire est maximale quand r est maximal et r’ minimal (ou inversement), c'est-à-dire quand r = et r’ = .

On obtient alors S_max = [(6 - 4)a² - (-1 + )²a²] = (9-6)a².

Télécharger la figure GéoPlan deux_cercles.g2w

10. Aire d'un rectangle inscrit dans un triangle

ABC est un triangle rectangle et isocèle en C tel que AB = 10.
J est le milieu de [AB] et M est un point de [AJ]. On note x la longueur AM.
On construit le rectangle MNPQ inscrit à l'intérieur du triangle ABC : N sur [AC] ; P sur [BC] et Q sur [JB].

1) Exprimer les longueurs MN et MQ en fonction de x.
2) On note A(x) l'aire du rectangle MNPQ. Exprimer A(x) en fonction de x et montrer que A(x) = −2(x - 5/2)² + 25/2.
3) Étudier le sens de variation et dresser le tableau de variation de la fonction A sur [0 ; 5].
4) Quelle est la position du point M sur [AB] pour laquelle l'aire du rectangle MNPQ est maximale ?

Télécharger la figure GéoPlan rct_ds_triangle.g2w