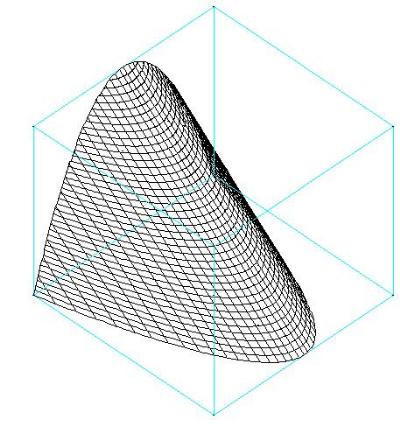
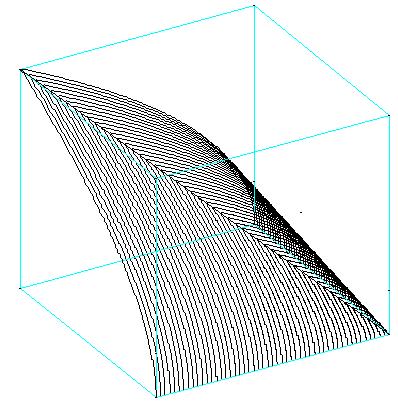
|
Surfaces dans l'espace au lycée en spécialité de TS - Réalisation avec GéoSpace. | ||
 Quadriques et GéoSpace |
| |
Sommaire1. Solides de révolution engendrés par des cercles |
3. Paraboloïde à selle | ||
|
Si vous ne visualisez pas l'image dans le cadre ci-contre, les contrôles ActiveX du CREEM ne sont pas installés sur votre PC. Vous pouvez :
page no 30, réalisée le 28/1/2003 - mise à jour le 29/8/2003 | |||
Terminale S | Derive | ||
Les quadriques de l'espace sont des surfaces algébriques de degré 2. Elles possèdent beaucoup de propriétés analogues à celle des coniques.
L'équation réduite permet de classifier ces surfaces avec les paramètres a, b, c :
Ellipsoïde : x2/a2 + y2/b2 + z2/c2 = 1.
Paraboloïde elliptique (bol) : z = x2/a2 + y2/b2.
Paraboloïde hyperbolique (à selle) : z = x2/a2 - y2/b2
; par un changement de variable, l'équation se transforme en z = xy.
Hyperboloïde à une nappe : x2/a2 + y2/b2 - z2/c2 = 1.
Hyperboloïde à deux nappes : x2/a2 + y2/b2 - z2/c2 + 1 = 0.
Cône basé sur une ellipse : x2/a2 + y2/b2 - z2/c2 = 0.
Toutes ces surfaces, sauf le paraboloïde hyperbolique, seront étudiées ici comme engendrées par des solides de révolution avec a = b.
Le programme de spécialité de terminale S propose l'étude des paraboloïdes d'équations z = x2
+ y2 et z = xy.
Les autres surfaces sont données à titre d'activités ou d'exercices.
1. Solides de révolution engendrés par des cercles
Paraboloïde elliptique (bol)
Le paraboloïde de révolution est la forme prise par la surface d'un liquide placé dans un cylindre d'axe vertical et animé d'une rotation rapide.
Conformément au programme de S, étudions le solide de révolution d'équation z = x2 + y2.
Pour une valeur positive fixée z0, x² + y² = z0 est l'équation d'un cercle c0
de centre I0(0 ; 0 ; z0) et de rayon ![]() , contenu dans le plan P0 d'équation z = z0.
, contenu dans le plan P0 d'équation z = z0.
Quand on fait varier z0, on obtient une succession de cercles qui « s'empilent » et engendrent ainsi une surface de révolution autour de l'axe oz.
Avec GéoSpace passer en mode Trace (icône ci-contre de la barre d'outils) |
|
|
Faire varier z0, avec les flèches du clavier pour construire le paraboloïde. | |
|
Sortir du « mode trace » (bouton ci-contre de la barre d'outils) pour toute autre action sur la figure. |
|
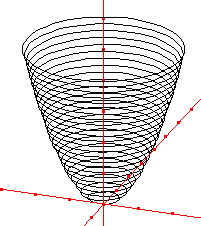 |
Voici le programme GéoSpace permettant d'obtenir la figure de gauche engendrée par des cercles : z0 réel libre de [0,5] Objet libre z0, paramètre: 3.6 P0 plan d'équation Z=z0 dans le repère Rxyz I0 point de coordonnées (0,0,z0) dans le repère Rxyz c0 cercle de centre I0 et de rayon rac(z0) dans le plan P0 (unité Uxyz) Objet libre actif au clavier: z0 Sélection pour trace: c0 Noms des points non affichés Il est aussi possible, comme ici à droite, de générer la figure par des paraboles isométriques contenues dans les plans P0 d'équation X=x0, parallèles au plan yoz. La parabole a pour équation z = y² + x0². | 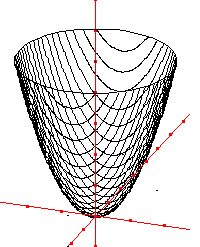
|
Génération par des paraboles : télécharger la figure GéoSpace parabol3.g3w
Exemple de figure interactive sans utiliser le mode trace
Le diamètre du cercle est donné par la fonction f(z).
La borne de départ est a, la borne de fin est b ; z0 est calculé pour 20 valeurs de [a, b].
Ellipsoïde
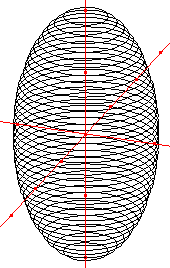 |
C'est une surface de l'espace, d'équation de la forme : x2/a2 + y2/b2 + z2/c2 = 1. Choisissons a = b = 1 et c = 2 pour étudier l'ellipsoïde de révolution d'équation : 4 x2 + 4 y2 + z2 = 4. Dans le programme GéoSpace précédent, modifier les deux lignes suivantes : z0 réel libre de [-2,2] … c0 cercle de centre I0 et de rayon rac(4-z0^2)/2 dans le plan P0 (unité Uxyz) |
![]() Télécharger la figure GéoSpace ellipsoi.g3w
Télécharger la figure GéoSpace ellipsoi.g3w
Cône
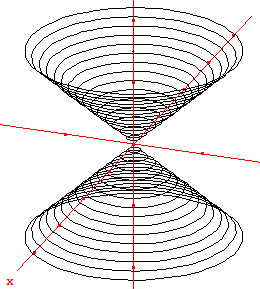 |
C'est une surface de l'espace, d'équation de la forme : x2/a2 + y2/b2 = z2/c2. Choisissons a = b = c = 1 pour étudier le cône de révolution d'équation : x2 + y2 = z2. Dans le programme GéoSpace modifier les deux lignes suivantes : z0 réel libre de [-2,2] |
![]() Télécharger la figure GéoSpace cone_rev.g3w
Télécharger la figure GéoSpace cone_rev.g3w
Sommaire
Faire de la géométrie dynamique
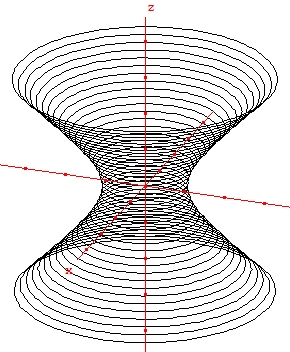
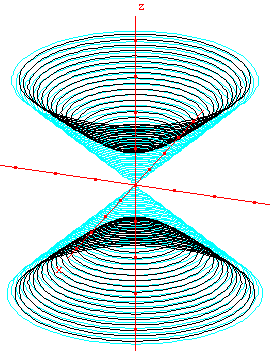
2. Hyperboloïde
Ce sont des surfaces de l'espace du type :
Hyperboloïde à une nappe : x2/a2 + y2/b2 - z2/c2 = 1 ;
avec le cône asymptote « interne » d'équation x2/a2 + y2/b2 - z2/c2 = 0.
Hyperboloïde à deux nappes : x2/a2 + y2/b2 - z2/c2
+ 1 = 0 ; avec le cône asymptote « externe » d'équation x2/a2
+ y2/b2 - z2/c2 = 0.
Choisissons a = b = 1 et c = 1 ou c = −1 pour étudier deux hyperboloïdes de révolution avec leurs cônes asymptotes d'équation x2 + y2 = z2.
a. Génération par des cercles
À une nappe
Étude du solide de révolution d'équation : x2 + y2 = z2 + 1.
|
À deux nappes
Étude du solide de révolution d'équation : x2 + y2 = z2 - 1. En bleu le cône asymptote.
|
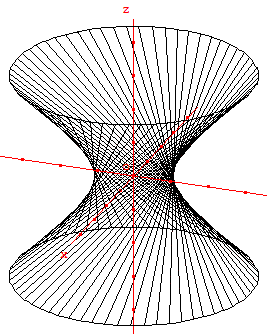
 b. Génération de l'hyperboloïde à une nappe par des droites
b. Génération de l'hyperboloïde à une nappe par des droites
On se place dans le plan d'équation x = 1. L'intersection de l'hyperboloïde avec ce plan vérifie
y2 - z2 = 0, soit en factorisant (y - z) (y + z) = 0.
L'intersection est donc la réunion de deux droites génératrices :
(d) de couple d'équations {x = 1 ; y - z = 0} et (d’) de couple d'équations {x = 1 ; y + z = 0}.
Toute rotation d'axe Oz transforme les droites (d) et (d’) en deux génératrices de l'hyperboloïde.
Représentation dans le cube [-3, 3]3 avec GéoSpace :
La droite (d) passe le point A(1, 3, 3) situé sur le cercle c0 du plan horizontal d'équation z = 3 et le point B(1, -3, -3) sur le cercle c1 du plan horizontal d'équation z = −3.
Une rotation d'axe Oz, d'angle t radians, transforme A en C et B en D. La droite (CD) est une génératrice du solide.
Château d'eau des Pialoux (26 La Roche-de-Glun) : les directrices renforcent la solidité de l'édifice et permettent une construction plus économique avec des fers à béton rectilignes.
Une génératrice
Trace des segments de génératrice [CD].
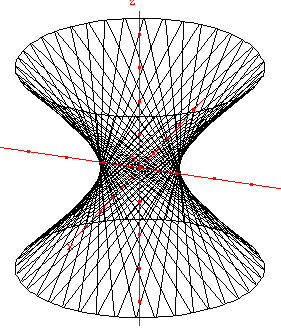
| Deux génératrices
La droite (d’) passe par les points A’(1, -3, 3) et B’(1, 3, -3). Une rotation d'axe Oz, d'angle t radians, transforme A’ en E et B’ en F. La droite (EF) est aussi une génératrice du solide.
|
 Remarque 1 :
Remarque 1 :
pour l'hyperboloïde à une nappe, l'existence de ces génératrices assure en architecture la
rigidité du solide permettant d'utiliser cette forme pour des châteaux d'eau ou des tours de refroidissement.
Remarque 2 :
dans le cas général avec le type x2/a2 + y2/b2
- z2/c2 = 1 on se ramène à un solide de révolution x2/a2
+ y2/a2 - z2/c2 = 1 par une affinité de plan Oxz
et de rapport b/a puis on fait une étude similaire en étudiant l'intersection avec le plan d'équation x = a2.
Sommaire
Faire de la géométrie dynamique
Figures interactives
Cliquer sur une figure.
Taper sur T pour activer le mode Trace,
faire varier z0, avec les flèches du clavier,
taper éventuellement sur S pour Sortir du mode trace.
Paraboloïde elliptique |
Paraboloïde elliptique engendré par des paraboles |
Ellipsoïde | Cône de révolution |
Hyperboloïde à une nappeTouche C : cacher/montrer le Cône asymptote. |
Hyperboloïde à deux nappesTouche C : Cône de révolution asymptote. |
Hyperboloïde à une nappe
|
Deux génératricesDéplacer les segments de génératrices [CD] et [EF]. |
Sommaire
Faire de la géométrie dynamique
3. Paraboloïde à selle :
Paraboloïde hyperbolique d'équation z = xy
Exemple de surface, du programme de spécialité de terminale S, qui n'est pas de révolution.
On utilise la méthode avec la construction d'une hyperbole (h0) dans le plan P0 d'équation z = z0.
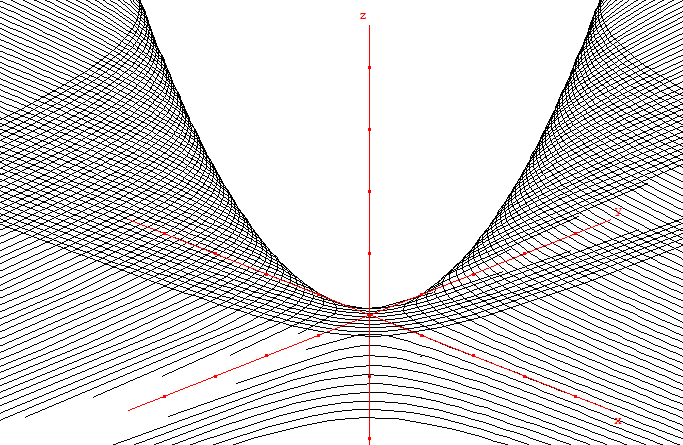
![]() télécharger la figure GéoSpace par_xy.g3w
télécharger la figure GéoSpace par_xy.g3w
Sommaire
Faire de la géométrie dynamique
Paraboloïde à selle ; figures interactives
Paraboloïde hyperbolique d'équation z = xy ; génération par des hyperboles
Cliquer sur la figure.
Taper sur T pour activer le mode Trace,
faire varier z0, avec les flèches du clavier,
taper éventuellement sur S pour Sortir du mode trace.
![]() Télécharger la figure GéoSpace par_xy.g3w
Télécharger la figure GéoSpace par_xy.g3w
Exemples de représentations dans le cube [-5,5]3
Il est conventionnel de représenter les surfaces à l'intérieur d'un cube. Ici on choisit le demi-côté a = 5.
Comme ci-dessus taper sur T pour activer le mode Trace,
faire varier z0, avec les flèches du clavier,
taper éventuellement sur S pour Sortir du mode trace.
|
Dans la figure ci-dessous sont représentés les arcs d'hyperboles situées dans les plans d'équations :
|
Sur l'hyperbole, située sur la face supérieure du cube, sont placés les points
P(x, a/x, a) et R(-x, -a/x, a) et sur la face inférieure les
points Q(x, -a/x, -a) et S(-x, a/x, -a). Les segments [PQ],
[RS], sont inclus dans le paraboloïde.
|
Ci-dessous deux représentations permettant de visualiser les arcs d'hyperboles et les segments de droite contenus dans le paraboloïde.
Il possible de changer les vues :
Cliquer sur une figure,
maintenir le click droit appuyé et déplacer la souris pour faire tourner la figure.
Il est aussi possible d'utiliser les flèches du clavier en maintenant la touche MAJ enfoncée.
|
|
|
Génération du paraboloïde hyperbolique d'équation z = xy par des droites
Représentation dans le cube [-1, 1]3
L'intersection de la surface avec les faces latérales du cube est formée par les quatre diagonales des faces de ce cube.
Les droites joignant les points de mêmes abscisses situés sur les diagonales opposées sont des génératrices de la surface.
Cliquer sur une figure,
maintenir le click droit appuyé et déplacer la souris pour faire tourner la figure.
La recherche de l'intersection de la surface précédente, avec le plan d'équation x = 0, permet d'en déduire l'étude de la surface d'équation :
z | |
y= | |
x |
![]() Télécharger la figure GéoSpace par_xy_2.g3w
Télécharger la figure GéoSpace par_xy_2.g3w
Sommaire
Faire de la géométrie dynamique
4. Paraboloïde hyperbolique d'équation x2 + y + z = 0
Représentation dans le cube [-2,2]3
|
Cliquer sur la figure de droite,
taper sur T pour activer le mode trace et se déplacer avec les flèches du clavier,
taper éventuellement S pour Sortir du mode trace.
 La symétrie par rapport au
plan d'équation y = 0 permet de visualiser la surface d'équation :
La symétrie par rapport au
plan d'équation y = 0 permet de visualiser la surface d'équation :
z = y - x2.
![]() Télécharger la figure GéoSpace p_x2_y_z.g3w
Télécharger la figure GéoSpace p_x2_y_z.g3w
Sommaire
Faire de la géométrie dynamique
5. Surface d'équation z = 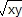
L'équation de cette surface peut aussi s'écrire sous la forme z2 = xy et z ≥ 0.
Représentation dans le cube [0,5]3
|
Cliquer sur la figure de droite,
taper sur T pour activer le mode trace et créer les demi-paraboles avec les flèches du clavier,
taper éventuellement sur S pour Sortir du mode trace.
![]() Télécharger la figure GéoSpace p_rac_xy.g3w
Télécharger la figure GéoSpace p_rac_xy.g3w
…avec |
La terminale |
GéoSpace |
GéoSpace 2nde | ||
Sommaire1. Solides de révolution engendrés par des cercles |
Faire de la géométrie dynamiqueSuggestions, remarques, problèmes : me contacter. | ||||