Géométrie plane en TS avec GéoPlan Géométrie plane en terminale S : deux exercices et le calcul approché d'intégrales avec GéoPlan.	Faire de la géométrie dynamique

1. Famille de cercles

ÉduSCOL - Terminale S - Banque de sujets 2007 - Sujet 030

Dans le plan on considère un triangle BOA rectangle en O et une droite (d) passant par O.
On note A’ et B’ les projetés orthogonaux respectifs de A et de B sur (d).
Enfin, dans le triangle OAB, H est le pied de la hauteur issue de O.

(a) Faire une figure à l'aide d'un logiciel de géométrie.
(b) Quelle conjecture peut-on faire concernant les différents cercles (c) lorsque la droite (d) tourne autour de O ?

On considère la similitude directe S de centre H qui transforme A en O.

• Quel est l'angle de cette similitude ? Justifier que l'image de O par S est B.
• Déterminer les images par S des droites (AA’) et (d), puis celle du point A’.
• Démontrer la conjecture faite au (b).

Conjectures

Les cercles (c) passent par le point H pied de la hauteur issue de O du triangle BOA.

Dans le cercle de diamètre [OA], les angles inscrits OAH et OA’H sont égaux, de même dans le cercle de diamètre [OB], les angles inscrits OBH et OB’H sont égaux. Les triangles BOA et B’HA’ sont semblables, donc B’HA’ est un triangle rectangle en H inscrit dans le cercle de diamètre [A’B’] : (c) contient le point H.

Si J, K et L sont les milieux des côtés [AB], [OB] et [OA], les centres I des cercles (c) appartiennent au cercle de diamètre la médiane [OJ] (cercle passant par K et L).

En effet, dans le cercle (c) l'angle au centre A’IH est la moitié de l'angle inscrit A’B’H. De même, dans le cercle de diamètre [AB], l'angle au centre OJA est la moitié de l'angle inscrit OBA.
Comme dit ci-dessus les angles inscrits A’B’H = OBA sont égaux, donc les angles doubles OIH et OJH sont égaux. Les points I, J, O et H sont cocycliques. Le point I est sur le cercle diamètre [OJ].

Commande GéoPlan

Déplacer le centre I.

Télécharger la figure GéoPlan famille_cercle.g2w
Voir aussi un curieux point de concours sur la hauteur OH : produit scalaire

Compétences évaluées
Compétences TICE
– Utilisation d'un logiciel de géométrie dynamique pour conjecturer une propriété.
Compétences mathématiques
– Triangles semblables ;
– Propriété de conservation d'une similitude (image d'une droite par une similitude) ;
– Triangle rectangle inscrit dans un demi-cercle.

2. Recherche d'un lieu géométrique

ÉduSCOL - Terminale S - 2007 - Sujet 002

Dans le plan (P), on donne quatre points O, A, B et C et un cercle (Γ) de centre O.
Le point M est un point quelconque variable sur le cercle (Γ).

On lui associe l'unique point M’ du plan (P) défini par l'égalité : = α + β + γ où α, β, γ sont des réels donnés.

1. Il s'agit de déterminer, dans un cas particulier, le lieu géométrique (L) du point M’ lorsque le point M décrit le cercle (Γ).

• À l'aide d'un logiciel de géométrie plane construire les points O, A, B et C, le cercle (Γ) et un point libre M sur ce cercle.
  Construire le point M’ associé à M.
• En observant plusieurs positions du point M faire une conjecture sur la nature de la transformation du plan qui transforme M en M’ ainsi que la nature du lieu géométrique du point M’.

2. (a) Déterminer par le calcul la nature de la transformation du plan qui transforme le point M en le point M’.
(b) Déterminer le lieu géométrique (L) du point M’.

Production demandée

• La figure réalisée avec le logiciel de géométrie dynamique.
• Le calcul permettant d'obtenir la nature de la transformation.
• La caractérisation du lieu géométrique de M’ et sa justification.

Commandes GéoPlan
Touche T : Tracé point par point du lieu,
touche S pour Sortir du mode trace,
touche L : dessin en bloc du Lieu.

Compétences évaluées
Compétences TICE
– Réaliser des constructions avec un logiciel de géométrie dynamique ;
– Tester les conjectures émises.
Compétences mathématiques
– Utiliser la notion de barycentre et ses propriétés ;
– Utiliser les transformations géométriques usuelles.

Télécharger la figure GéoPlan lieu_barycentre.g2w
Sommaire
Faire de la géométrie dynamique

3. Barycentre

ÉduSCOL - Terminale S - 2007 - Sujet 026

Situation

On considère A, B et C trois points non alignés du plan et k un réel de l'intervalle [-1; 1].
On note G_k le barycentre du système de points pondérés : {(A, α_k) ; (B, β_k) ; (C, γ_k)}

où α_k, β_k et γ_k sont des réels dépendants de k, de somme non nulle. Il s'agit de déterminer le lieu des points G_k lorsque k décrit l'intervalle [-1; 1].

Fiche élève

On considère A, B et C trois points du plan et k un réel de l'intervalle [-1; 1].
On note G_k le barycentre du système de points pondérés : {(A, k² + 1) ; (B, k) ; (C, -k)}.
Le but de cet exercice est de déterminer le lieu des points G_k lorsque k décrit l'intervalle [-1; 1].

1. Visualisation à l'aide d'un logiciel de géométrie :

• Construire les points A, B, C, G₁ et G_-1.
• Construire le point G_k puis visualiser l'ensemble des points G_k lorsque k décrit [-1; 1].
• Quelle est la nature de l'ensemble précédent ?

2. Justification mathématique :

• Justifier, pour tout réel k de [-1; 1] l'existence du point G_k.
• Démontrer que pour tout réel de l'intervalle [-1; 1], on a: = .
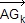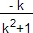
• Démontrer la conjecture faite avec le logiciel. On pourra utiliser les variations de la fonction f définie sur [-1; 1] par : .

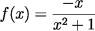Commandes GéoPlan
Touche T : Trace du point G_k,
touche S pour Sortir du mode trace,
touche L : dessin en bloc du lieu de G_k.

Indications

D'après la fonction vectorielle de Leibniz α + β + γ = (α + β + γ) , en plaçant M en A on a :
( k² + 1) = k - k = −k et = .

La fonction f est continue et décroissante sur [-1; 1].

Télécharger la figure GéoPlan barycentre.g2w
Figure classique : voir épreuve pratique

4. Partage d'un triangle

ÉduSCOL - Terminale S - 2007 - Sujet 047

Dans le plan on définit un triangle ABC non isocèle en A et dont les angles en B et en C sont aigus. On note a son aire.
On appelle H le pied de la hauteur issue de A dans le triangle ABC et l'on se place dans le cas où CH > BH.

On se propose de démontrer qu'il existe une droite et une seule perpendiculaire au côté [BC], en un point M, qui partage le triangle ABC en deux polygones de même aire.

• Construire la figure demandée en utilisant un logiciel de géométrie dynamique. Déterminer, à l'aide du logiciel, la position de M en lequel la droite recherchée doit couper le segment [CH] pour répondre au problème posé.
• Étudier le cas où le point M est sur le segment [BH].
• On suppose que le point M est situé sur le segment [CH] et on pose CM = x. On appelle N le point d'intersection du segment [AC] avec la droite perpendiculaire à (BC) passant par M.

On note L la longueur du segment [CH]. On admet que la fonction f qui, à tout x de [0; L], associe l'aire du triangle CMN est continue.
On ne cherchera pas à expliciter f(x).

(a) Que traduit l'égalité f(x) = ?

• Préciser les variations de f à l'aide du logiciel. Déterminer la valeur de f(0).
• Comparer f(x) et 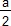quand M est en H.
• En déduire la réponse au problème posé.

Production demandée

• Figure réalisée avec emplacement du point M répondant au problème.
• Interprétation de l'égalité (a).
• Utilisation d'un théorème d'analyse.

Indications

f(0) = 0, f(L) > lorsque M est en H, comme f est continue sur [0; L], d'après le théorème des valeurs intermédiaires, il existe une valeur x pour laquelle f(x) = .
Le triangle CMN a alors une aire égale à la moitié de celle de ABC.

Pour l'aire du triangle CMN solution on a : x × MN = , d'où MN = .

Les triangles rectangles NMC et AHC sont semblables don tan(C) = = , soit = , d'où x = .

x = CM, y = f(x) = Aire(CMN), dans le cadre de droite est représenté le point S(x, y).

Commandes GéoPlan : Le déplacement de M se fait au clavier ou à la souris.
La touche L fait apparaître (ou disparaître) le lieu de S.

Touche T : Tracé point par point du graphe,
touche S pour Sortir du mode trace,
touche A : solution.

Télécharger la figure GéoPlan max_aire_tr_peri_const.g2w
Figure classique : voir épreuve pratique
Sommaire
Faire de la géométrie dynamique

Intégration

Intégrale de f entre a et b par la méthode des rectangles

f(x) =

Avec le menu : créer>numérique>fonction numérique>une variable, modifier la fonction f.

Pour chaque calcul cliquer dans la figure et taper S pour START.

Calcul d'une valeur approchée d'intégrale avec GéoPlan

On décompose le segment [a, b] en n segment de même longueur h = (b-a)/n et on note u₀ = a, u₁, u₂, u₃ …, u_n = b. La suite des extrémités de ces intervalles.

Pour une valeur x₀ égale à un des u_i on trace deux extrémités A(x₀, 0) et A’(x₀+h, 0) sur l'axe (Ox),
Les points M(x₀, f’(x₀)) et M’(x₀+h, f’(x₀)) permettent de tracer le rectangle AA’M’M nommé R.
Les points N(x₀, f’(x₀+h)) et N’(x₀+h, f’(x₀+h)) permettent de tracer le rectangle AA’N’N nommé R’.

Technique GéoPlan

Après le tracé du premier rectangle de côté A(a, 0)A’(a+h, 0), on répète, avec la commande S, n-1 fois le tracé des rectangles en activant le mode Trace.
La commande Cm2 itére le calcul de I, avec l'astuce que le calcul se fait avant l'affectation de x₀+h à x₀, la hauteur du rectangle R est donc f’(x₀+h) et celle du rectangle R’ est donc f’(x₀+ 2h).

Commandes GéoPlan :

Éventuellement, changer a, b, n en les pilotant au clavier :
taper A pour modifier a au clavier,
taper B pour modifier b,
taper N pour modifier n.

Couplage Touches / Commandes :

Touche I : INITIALISATION : cette touche couple 2 commandes :
Cm0 : Sortie du mode Trace
Cm1 : Initialisation de x0, I à a, 0

Touche T : ITERATION Cm2 : x0 devient x0+h et I devient I+h*f(x0+h)

Touche S : START : cette touche couple 4 commandes : L'initialisation et :
Cm3 : on garde la trace du rectangle R
Cm4 : on répète la commande Cm2 n-1 fois

Terminer le mode trace à la fin du tracé avec la commande F pour retrouver les commandes GéoPlan.

Encadrement

Comme en mode trace, un rectangle AA’N’N efface le rectangle AA’M’M précédent, il faut deux programmes distincts pour les fonctions croissantes sur [a, b] et pour les décroissantes.

Pour chaque calcul cliquer dans la figure et taper S pour START.

Méthode des trapèzes

Une valeur approchée de l'intégrale se trouve en faisant la somme des aires des trapèzes AA’M’M de sommets, pour une valeur x₀, les points A(x₀, 0) et A’(x₀+h, 0) sur l'axe (Ox) et les points M(x₀, f’(x₀)) et M’(x₀+h, f’(x₀+h)).

Pour la fonction f(x) = étudiée ci-contre sur [0, 1],
on a une excellente approximation sachant que ≈ 0,7853.

Télécharger la figure GéoPlan tsaire_trapeze.g2w