L'espace en TS - Figures interactives avec GéoSpace Banque de sujets 2007 de l'Épreuve pratique, publiés par ÉduSCOL - Mathématiques.

Faire de la géométrie dynamique

Sujets ÉduSCOL

1. Perpendiculaire commune à deux droites

ÉduSCOL - Terminale S - Banque de sujets 2007 - Sujet 015

Situation

On définit, dans l'espace, deux droites particulières (d₁) et (d₂) non coplanaires.
On désigne par M un point variable de la droite (d₁) et par N un point variable de (d₂). Il s'agit de déterminer le minimum de la distance MN.

Télécharger la figure GéoSpace dist_2_droites.g3w

Déplacer les points M et N afin de déterminer le minimum de la distance MN.

Commandes GéoSpace
Taper T pour activer le mode Trace du point S,
S, pour Sortir du mode trace,
P, pour tracer la perpendiculaire commune.

Déplacer les droites (d₁) et (d₂) en cliquant sur les extrémités des segments les représentant.

Fiche élève

• L'espace est rapporté à un repère orthonormal.
  À l'aide d'un logiciel de géométrie dans l'espace, faire figurer les points A(-2 ; -2 ; 0) ; B(1 ; 1 ; 0) ; C(1 ; -1 ; 1) et D(-1 ; 1 ; 1), les droites (AB) et (CD),
  un point M mobile sur la droite (AB) et un point N mobile sur la droite (CD).

• Afficher la distance MN et essayer de placer des points M et N de façon à minimiser cette distance.
  Donner une valeur approximative de cette distance minimale.

• Combien de couples de points (M ; N) répondant à cette condition de distance minimale semble-t-il y avoir ? Afficher les coordonnées de ces points.
• Quelles semblent être les positions respectives des droites (MN) et (AB) d'une part, et (MN) et (CD) d'autre part ?
  Mettre en évidence cette conjecture, à l'aide du logiciel.
  Calculer MN². (On pourra écrire = t et = k ).
  Vos résultats confirment-ils certaines de vos conjectures ?

Indications

= + + = − t + + k avec (3 ; 3 ; 0), (3 ; 1 ; 1) et (-2 ; 2 ; 0),
d'où (-3t + 3 -2k ; -3t + 1 + 2k, 1)
et MN² = (-3t + 3 -2k)² + (-3t + 1 + 2k)² + 1².

MN est minimal si -3t + 3 -2k = 0 et -3t + 1 + 2k = 0. Ce système admet la solution t = et k = correspondant aux points M(0 ; 0 ; 0) et N(0 ; 0 ; 1).

MN = 1 et (0 ; 0 ; 1) est orthogonal à et ; la droite (MN) est la perpendiculaire commune à (AB) et (CD).

Télécharger la figure GéoSpace dist_2_droites3.g3w

Commentaires : les droites sont deux diagonales de faces d'un parallélépipède rectangle dont les côtés sont parallèles aux axes. Ces calculs sont un peu compliqués en regard de la facilité des droites données. Et encore, le texte original proposait O comme point A et le point de coordonnées (0 ; 0 ; 1) pour D : Quelle note mériterait l'élève qui, sans calcul, remarquerait que les deux droites sont contenues dans les plans d'équations z = 0 et z = 1. OD = 1, étant égal à distance des deux plans, est la distance minimale entre les deux droites ?

Télécharger la figure GéoSpace dist_2_droites4.g3w

Tracé de la perpendiculaire commune à deux droites

(d₁) et (d₂) étant deux droites non coplanaires de l'espace, il existe une droite et une seule, perpendiculaire à ces deux droites.

Pour la construire, la méthode consiste à choisir un point A sur (d₁) et à tracer une droite (d₃) parallèle à (d₂) passant par A. Les droites (d₁) et (d₃) déterminent un plan (p) contenant A.
Soit (Δ) la perpendiculaire commune à (d₁) et (d₃) passant par A. (Δ) est la perpendiculaire en A au plan (p). (Δ) et (d₁) déterminent un plan (q) perpendiculaire à (p).
Le plan (q) coupe (d₂) en N. Dans le plan (q), la parallèle à (Δ) passant par N coupe (d₁) en M.
(MN) est la perpendiculaire commune recherchée. MN est la distance minimale entre deux droites.

Commandes GéoSpace
Déplacer les droites (d₁) et (d₂) en cliquant sur les extrémités des segments les représentant.
Déplacer les profils des plans (p), (q) ou la marque (d₃) en déplaçant leurs points d'ancrage.

Télécharger la figure GéoSpace dist_2_droites2.g3w

Compétences évaluées
Compétences TICE
– Construire une figure à l'aide d'un logiciel de géométrie dans l'espace ;
– Utiliser l'aspect dynamique pour faire des conjectures.
Compétences mathématiques
– Connaître la représentation paramétrique d'une droite ;
– Maîtriser l'orthogonalité dans l'espace.

2. Section plane d'un tétraèdre et optimisation d'une distance

ÉduSCOL - Terminale S - Banque de sujets 2007 - Sujet 033

Situation

Dans l'espace, on donne un tétraèdre OABC et le milieu I de [AB]. Soit M un point quelconque du segment [AC]. Le plan passant par I et orthogonal à la droite (IM) coupe la droite (OB) en N. On cherche à minimiser la distance MN.

Technique GéoPlan

Avec les menus de GéoSpace, on ne peut pas calculer la longueur d'un segment, mais taper directement dans le texte de la figure :

y = MN

La figure de gauche, section_tetraedre, importe(Menu >Piloter>Importer) la valeur de x, de la figure de droite. x doit être défini comme réel non borné dans cette figure, bien qu'il soit borné entre 0 et 1 dans tetraedre_fct (pour permettre d'afficher la courbe comme lieu de points).

Dans tetraedre_fct le tétraèdre et sa section sont dupliqués, en mode non dessiné, pour réaliser le calcul de y.
Pour obtenir un axe (Ox) horizontal, le graphe est réalisé avec le plan (oxz) de face correspondant à l'instruction :

Rotations de Rxyz: verticale: 90 horizontale: 0 frontale: 0

Compétences évaluées

Compétences TICE
– Constructions géométriques et mesures avec un logiciel de géométrie dynamique.
Compétences mathématiques
– En géométrie analytique, calcul de la distance de deux points de l'espace ;
– Recherche d'un extremum d'une fonction.

3. Plans perpendiculaires

ÉduSCOL - Terminale S - Banque de sujets 2004 - Sujet 11

L'espace est rapporté à un repère orthonormal (O, , , ).
• Déterminer une équation du plan P passant par le point A(1, 0, 1) et de vecteur normal (-1, 1, 1).

• Soit P’ le plan d'équation x + 2y - z + 1 = 0 et M le point de coordonnées (0, 1, 1).
Sachant que deux plans sont perpendiculaires si un vecteur non nul normal à l'un est orthogonal à un vecteur non nul normal à l'autre, démontrer que les plans P et P’ sont perpendiculaires.

Calculer les distances d et d’ du point M aux plans P et P’ respectivement.

• Donner une représentation paramétrique de la droite D intersection des plans P et P’.

Déterminer les coordonnées du point H de D tel que la droite (MH) soit perpendiculaire à la droite D.

Vérifier que MH² = d² + d’².

Télécharger la figure GéoSpace plans_perpendiculaires.g3w

Indications

GéoSpace permet de faire la figure et de réaliser des calculs.

En plaçant le point B de coordonnées (0, 1, 2), le plan P est alors orthogonal au vecteur et a pour équation -x + y + z = 0.
Le plan P’ a pour vecteur normal ’(1, 2, -1). Le produit scalaire .’= −1×1 + 1×2 + 1×(-1) est nul, les vecteurs sont orthogonaux et les plans P et P’ sont perpendiculaires.
Le point N, projection orthogonale de M sur P, a pour coordonnées (, , ) car est un vecteur directeur de la droite (MN) ; MN² = .
Le point N’, projection orthogonale de M sur P’, a pour coordonnées (-, , ) ; MN’² = .

Les équations paramétriques de la droite D sont : x = k, y = − , z = k +.
Le plan Q passant par M orthogonal à D a pour équation x + z = 1.
Pour k =, on trouve le point H de coordonnées (, -, ) ; MH² = 2. [HM] est la diagonale du rectangle MNHN’. MH² = d² + d’² se vérifie par une relation de Pythagore.

4. Orthogonalité dans le cube

On considère un cube ABCDEFGH, d'arête de longueur a (a réel strictement positif).
Soit I le point d'intersection de la droite (EC) et du plan (AFH).

Problème d'incidence

Montrer que la droite (EC) est perpendiculaire au plan (AFH).

Produit scalaire

ÉduSCOL - Terminale S - Banque de sujets 2004 - Sujet 23

1. Calculer, en fonction de a, les produits scalaires suivants :

., ., .

2. En déduire que les vecteurs et sont orthogonaux.
On admettra, de même, que les vecteurs et sont orthogonaux.

3. En déduire que le point I est le projeté orthogonal de E sur le plan (AFH).

4. Justifier les résultats suivants : les droites (AF) et (EH) sont orthogonales, ainsi que les droites (AF) et (EI).
En déduire que la droite (AF) est orthogonale à la droite (HI).
Établir, de même, que la droite (AH) est orthogonale à la droite (FI).

5. Que représente le point I pour le triangle AFH ?

Télécharger la figure GéoSpace cube3.g3w

Variante

La droite (AF) perpendiculaire à deux côtés du triangle BCE est perpendiculaire au plan (BCE) et en particulier à la droite (EC).
De même, la droite (FH) perpendiculaire à deux côtés du triangle CEG, est perpendiculaire au plan (CEG) et en particulier à la droite (EC).

(EC) perpendiculaire aux deux droites concourantes (AF) et (FH) est perpendiculaire au plan (AFH).

b. Généralisation

(EC) grande diagonale du cube est orthogonale aux plans (AFH) et (BDG). Ces deux plans sont parallèles.

La droite (EC) perce les triangles équilatéraux AFH et BDG en leurs centres I et J.

EI = IJ = JC.

Télécharger la figure GéoSpace cube2.g3w

c. Milieu

Si O est le milieu du carré ABCD, la droite (EO) rencontre le plan (AFH) au point K.

Ce point est le milieu de [EO].

Indication

Si O’ est le milieu du carré EFGH, dans le plan (EAC) K est le point d'intersection des diagonales du rectangle EAOO’.

Télécharger la figure GéoSpace cube4.g3w

Voir aussi coin de cube : GéoSpace en seconde

Sommaire
Faire de la géométrie dynamique

5. Tétraèdre

ÉduSCOL - Terminale S - Banque de sujets 2004 - Sujet 24

L'espace est rapporté à un repère orthonormal (O ; , , ). On considère les points A, B, C et S de coordonnées respectives :

A(-1, 0, 1) ; B(1, 4, -1) ; C(3, -4, -3) ; S(4, 0, 4)

1. Démontrer que le triangle ABC est un triangle rectangle en A.

2. a) Montrer que le vecteur est orthogonal aux vecteurs et .
b) En déduire une équation cartésienne du plan (ABC).

3. a) Démontrer que O est le barycentre des points A, B, C affectés de coefficients que l'on déterminera.

b) En déduire que O est situé dans le triangle ABC.

4. Calculer le volume V du tétraèdre SABC.

Indications

(2, 4, -2) ; (4, -4, -4) : . = 2 × 4 + 4 × (-4) + (-2) × (-4) = 0. Le produit scalaire est nul, les vecteurs sont orthogonaux. Le triangle ABC est un triangle rectangle en A.

(4, 0, 4) : . = 0 ; . = 0. , orthogonal aux vecteurs et , est orthogonal au plan (ABC).
Un plan perpendiculaire au vecteur (a, b, c) a une équation de la forme ax + by + cz = d. Une équation du plan (ABC) est donc x + y = 0.

4 + + = , O est le barycentre de (A, 4) ; (B, 1) ; (C, 1). Les coefficients sont positifs, O est à l'intérieur du triangle. OS est une hauteur du tétraèdre.

V = s(ABC) × OS = AB × AC × OS = 32.

Télécharger la figure GéoSpace tetraedre.g3w
Sommaire
Faire de la géométrie dynamique

Groupe de mutualisation

7. Perdu dans l'espace, les ambiguïtés de la perspective cavalière

On représente en perspective cavalière un cube ABCDEFGH et un point M selon la figure ci-contre.
Le point M est-il à gauche ou sur la droite du cube ci-contre ?

Indications

Cliquer dans la figure et taper 1 pour afficher/effacer un cube montrant que le point M peut représenter un point situé sur la droite (CD), à gauche.

Mais le dessin de deux cubes devant le cube initial (touche 2) montre que M peut représenter un point de la droite (GF), sur le côté droit du cube !

Si M₁ est le point de l'espace situé sur (CD) et M₂ est le point de l'espace situé sur (GF), le point M peut représenter n'importe quel point de la droite (M₁M₂).

Déplacer la figure puis taper F pour retrouver la vue de face avec le plan perpendiculaire à la droite (M₁M₂).

Télécharger la figure GéoSpace perdu_espace.g3w

Voir : activités

8. Solides définis par leurs équations

Exemples d'exercices pour l'articulation « première terminale » en série S

Dans l'espace muni d'un repère orthonormal.

Déterminer les solides définis par les équations suivantes :

a) x² + y² + z² = 4

b) x² + y² = 4

9. Distribuer une section déjà construite

Demander aux élèves de tracer les points « hors solide » qui ont permis d'obtenir cette section. Autrement dit, leur faire faire des exercices sur les sections dans les deux sens.

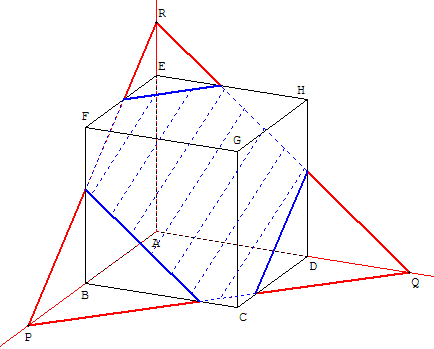
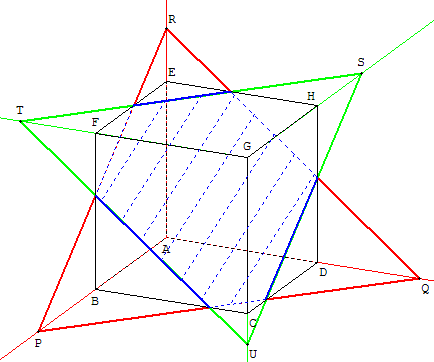
a. Section plane d'un cube par le plan (PQR)

Télécharger la figure GéoSpace section_cube.g3w

Commandes GéoSpace

Touche 1 : afficher /effacer le plan (PQR)
Touche 2 : afficher /effacer le plan (STU)
Touche 3: afficher /effacer la section plane

b. 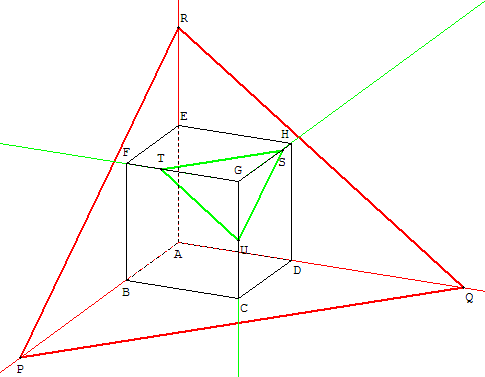Section triangulaire

Moins facile.

À partir du plan (PQR), trouver la section plane STU.

Dans l'autre sens, à partir de la section plane STU, retrouver les points P, Q et R situés sur les prolongements des côtés.

Voir correction dans Avec GéoSpace

Télécharger la figure GéoSpace section_cube2.g3w