Polygones réguliers avec GeoGebra

Sommaire

1. Polygone constructible
2. Polygone régulier : côtés, angles
5. Pentagone - Construction de Ptolémée
6. Hexagone
8. Octogone

Triangle équilatéral
Carré

Page n^o 93, créée le 30/8/2009

GéoPlan
Polygones réguliers

Les éléments d'Euclide

Le carré
au collège

Construction du pentagone régulier

Faire de la
géométrie dynamique
avec GeoGebra

Faire de la géométrie dynamique

1. Polygone constructible

Savoir construire un polygone régulier, à n côtés, c'est savoir construire le point de coordonnées (cos, sin ). Ayant ainsi construit un côté de ce polygone, il suffit de reporter de proche en proche sa longueur sur le cercle unité.

Les éléments d'Euclide donnent les constructions des polygones réguliers de 3, 4, 5, 6 et 15 côtés.

Ils expliquent comment, grâce à la construction des bissectrices, doubler le nombre de côtés d'un polygone.

Théorème de Gauss : Soit n et m deux entiers naturels premiers entre eux. Le polygone à nm côtés est constructible, à la « règle et au compas », si et seulement si les polygones à n côtés et à m côtés sont constructibles.

En effet, le théorème de Bezout permet de dire que si m et n sont premiers entre eux, il existe deux entiers relatifs u et v tels que um + vn = 1.
Multipliant cette expression par , il vient : u + v = .

On obtient l'angle , sur le cercle unité, en reportant u fois l'angle et v fois l'angle , angles que l'on sait construire.

Exemple - construction du polygone régulier à 15 côtés :
Comme on sait construire le triangle équilatéral et le pentagone régulier, 3 et 5 étant premiers entre eux, en multipliant par la relation de Bezout 2 × 3 - 5 = 1,
on obtient l'égalité 2 - = .
Sur un cercle, à partir d'un point A, on place un point G tel que (, ) = , le point B tel que (, ) = − est le deuxième sommet du polygone régulier de côté AB.

Il faudra attendre 1796 pour que Gauss démontre que le polygone de 17 côtés était aussi constructible à la règle et au compas.

Polygones constructibles

Un polygone régulier de n côtés est constructible si cos est un nombre constructible. n est alors une puissance de 2, un nombre premier de Fermat de la forme 1 + 2^(2k), un produit de nombres de Fermat ou un produit d'une puissance de 2 par des nombres de Fermat.

Pour n = 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20 … les polygones à n côtés sont constructibles. Pour n = 7, 9, 11, 13, 14, 18, 19 … ils ne le sont pas.

Voir :  solides de Platon

Bibliographie : Carrega J.-C. - Théorie des corps : la règle et le compas - Hermann 2001
Nombres constructibles - Edmond Jung - Bulletin AMEP n^o 458 - juin 2005

Sommaire
Faire de la géométrie dynamique

2. Polygone régulier

Un polygone régulier est un polygone inscrit dans un cercle et dont tous les côtés ont la même longueur et les angles la même mesure. Il peut être convexe ou croisé.

Un polygone régulier à n côtés se superpose à lui-même quand on le tourne d'un angle de .

Un polygone régulier convexe est composé de (n - 2) triangles. Si on additionne les angles de ces triangles, on obtient la somme des angles intérieurs du polygone. La somme des angles d'un polygone à n côtés est égale à
(n - 2) π .

Les rayons d'un polygone inscrit dans un cercle relient ses sommets à son centre. Les apothèmes relient les milieux de ses côtés à son centre.

Côtés

Angle au
centre

Angle
intérieur

Triangle équilatéral

3

120°

60°

Carré

4

90°

90°

Pentagone

5

72°

108°

diagonale/côté = Φ

Hexagone

6

60°

120°

côté = rayon du cercle circonscrit

Heptagone

7

Octogone

8

45°

135°

Ennéagone

9

40°

140°

Décagone

10

36°

144°

rayon/côté = Φ

Hendécagone

11

Dodécagone

12

30°

150°

Pantadécagone

15

24°

156°

n côtés

n

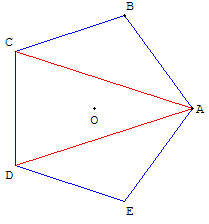
5. Pentagone - Construction de Ptolémée.

Désolé, l'applet GeoGebra ne peut pas démarrer, vérifier votre version Java.

Pour construire un pentagone régulier convexe inscrit dans un cercle à la « règle et au compas » il suffit de savoir construire un angle au centre de dont le cosinus est égal à .

Pour un pentagone inscrit dans un cercle de centre O, ayant un sommet A donné on peut effectuer la construction adaptée du procédé de création du rectangle d'or :

tracer un cercle (c₁) de centre O, de rayon r, passant par A(r, 0).
Placer un diamètre [AA’] et un rayon [OB’], perpendiculaire à [AA’].

K est le milieu de [OA’], le cercle (c₂) de centre K et de rayon KB’ coupe [OA] en U. La longueur du côté du pentagone est égale à B’U.

La médiatrice de [OU] coupe le premier cercle (c₁) aux points B et E qui sont deux sommets du pentagone. Le cercle de centre B passant par A recoupe (c₁) en C. Le symétrique D de C par rapport à (AA’) termine la construction du pentagone.

En effet, KB’ = KU = r , d'après la propriété de Pythagore, dans le triangle OKB’ rectangle en O, donc OU = r( - ) = et OI =  r.
L'angle (, ) a un cosinus égal à , c'est bien un angle de . La corde [AB] est donc le premier côté du pentagone régulier convexe ABCDE.

Le point B a pour coordonnées OI = r cos et IB = r sin .
Le point C a pour abscisse r cos = − r cos = − r,
et pour ordonnée r sin = r sin .

Voir : pentagone régulier :
    constructions exactes
    constructions approchées

6. Hexagone

Désolé, l'applet GeoGebra ne peut pas démarrer, vérifier votre version Java. Le côté de l'hexagone régulier inscrit dans un cercle est égal au rayon r de ce cercle.

Construction de l'hexagone à partir du cercle circonscrit

Pour inscrire un hexagone régulier dans un cercle, il suffit de porter six fois sur la circonférence une ouverture de compas égale au rayon et de joindre les points consécutifs ainsi obtenus.

Avec GéoPlan

Placer deux points O et A,
tracer le cercle (c) de centre O passant par A.

Le cercle de centre A passant par O coupe le cercle (c) en B et F,
le cercle de centre B passant par O recoupe le cercle (c) en C,
le cercle de centre C passant par O coupe le cercle (c) en D,
le cercle de centre D passant par O coupe le cercle (c) en E..

Effacer les cercles et tracer les côtés de l'hexagone ABCDEF.

Télécharger la figure GeoGebra hexagone.ggb
Télécharger la figure GéoPlan hexagone.g2w
Télécharger la figure Cabri hexagone.fig

Voir : construction d'un hexagone par pliage d'un triangle équilatéral
hexagramme mystique

8. Octogone

La longueur du côté est : 2 r sin = ≈ 0,765 r

Voir le calcul du sinus : angle trigonométrie

Octogone inscrit dans un cercle

Désolé, l'applet GeoGebra ne peut pas démarrer, vérifier votre version Java.

Tracer deux diamètres [AE] et [CG] perpendiculaires du cercle : ACEG est un carré.
Tracer les bissectrices de ces angles pour former deux autres diamètres :
les cercles de centres A et C passant par O se recoupe en I. (OI) est la médiatrice de [AC] coupe le cercle en B et F,
les cercles de centres C et E passant par O se recoupe en J. (OJ) est la médiatrice de [CE] coupe le cercle en D et H,
En joignant les extrémités des quatre diamètres, on obtient l'octogone régulier ABCDEFGH.

Télécharger la figure GeoGebra octogone.ggb
Télécharger la figure GéoPlan octogone.g2w

Octogone inscrit dans un carré

Désolé, l'applet GeoGebra ne peut pas démarrer, vérifier votre version Java.

Tracer les diagonales du carré et marquer le centre O du carré, point d'intersection des diagonales. Tracer alternativement les cercles centrés sur chaque sommet, passant par le centre O. En joignant les points d'intersection de ces cercles avec les côtés du triangle, on obtient un octogone régulier.

Télécharger la figure GeoGebra octogone2.ggb
Télécharger la figure GéoPlan octogone2.g2w

Sommaire
Faire de la géométrie dynamique

Faire de la
géométrie dynamique
avec GeoGebra

Grands problèmes de la géométrie grecque

Les éléments d'Euclide

Constructions du pentagone régulier

Cabri-géomètre
Classe de sixième

Le triangle équilatéral

Sommaire

1. Polygone constructible
2. Polygone régulier : côtés, angles
5. Pentagone - Construction de Ptolémée
6. Hexagone
8. Octogone

Triangle équilatéral
Carré

Faire de la géométrie dynamique

Accueil : http://www.maths.ac-aix-marseille.fr/debart

Suggestions, remarques, problèmes : me contacter.