Les configurations du plan : trois exercices avec GéoPlan.
	Le parallélogramme au collège	…avec GéoPlan

Quadrilatère convexe, concave, croisé

Un quadrilatère ABCD est un polygone qui a quatre côtés [AB], [BC], [CD] et [DA].
Les points A et C d'une part ; B et D d'autre part, sont les sommets opposés du quadrilatère.
Les diagonales [AC] et [BD] sont les segments qui joignent deux sommets opposés.

Un quadrilatère est convexe si les deux diagonales sont à l'intérieur du quadrilatère (le parallélogramme est convexe).
Un quadrilatère est concave si (au moins) une des diagonales est à l'extérieur du quadrilatère.
Un quadrilatère est croisé si les deux diagonales sont à l'extérieur du quadrilatère. Un quadrilatère croisé est concave (papillon).

Propriétés du parallélogramme

En classe de cinquième, les élèves doivent connaître et utiliser une définition et les propriétés (relatives aux côtés, aux diagonales et aux angles) du parallélogramme.

En privilégiant les transformations, on définit un parallélogramme comme quadrilatère dont les diagonales se coupent en leur milieu.

Le point d'intersection des diagonales d'un parallélogramme est son centre de symétrie (et son centre de gravité).
La symétrie centrale permet de justifier des propriétés caractéristiques du parallélogramme que les élèves doivent connaître :

• les côtés opposés sont parallèles,
• les côtés opposés sont la même longueur,
• les angles opposés ont la même mesure,
• les angles consécutifs sont supplémentaires (leur somme fait 180°).

Les diagonales partagent le parallélogramme en quatre triangles de même aire.

Télécharger la figure GéoPlan parallelogramme.g2w

Translation, vecteur

Avant 2008, en classe de troisième, était faite la liaison entre parallélogramme, translation et vecteur :

On peut définir la translation à partir du parallélogramme : dire que le point M’ est l'image du point M par la translation qui transforme A en B signifie que le quadrilatère ABM’M est un parallélogramme.
Définir le parallélogramme à partir de la translation : ABCD est un parallélogramme si la translation qui transforme A en B, transforme D en C.

On peut définir le vecteur à partir du parallélogramme : = si ABCD est un parallélogramme.
Définir le parallélogramme à partir de vecteur : ABCD est un parallélogramme si = .

Au collège et au lycée, on ne parle plus de classe d'équivalence de bipoints.

Propriétés caractéristiques

Les propriétés suivantes d'un quadrilatère sont équivalentes et définissent chacune un parallélogramme :

• Les côtés opposés sont parallèles deux à deux,
• le quadrilatère est convexe et les côtés opposés sont de même longueur, deux à deux,
• les diagonales se coupent en leur milieu,
• ABCD est un parallélogramme si = ,
• le quadrilatère est convexe et les angles opposés ont la même mesure deux à deux,
• les angles consécutifs sont supplémentaires deux à deux.

Contre-exemple montrant l'importance de la convexité : antiparallélogramme, quadrilatère croisé ayant ses côtés opposés de même longueur et ses angles opposés de même mesure.

1. Dessiner un parallélogramme à partir de trois sommets

Le but de ce chapitre est de dessiner des quadrilatères qui gardent leurs propriétés lorsque l'on déplace leurs sommets. En général, ces figures s'obtiennent à partir de trois points libres A, B et D. L'ordinateur calcule la position du point C (point lié qui ne peut pas être déplacé).

Placer trois points A, B et D, dessiner les segments [AB] et [AD], et trouver le point C qui complète le parallélogramme en utilisant une des quatre méthodes ci-dessous correspondant aux quatre définitions proposées plus haut.

Compléter le parallélogramme avec les segments [BC] et [DC],
gommer les constructions (non dessiné).

Commandes GéoPlan
Déplacer les points A, B ou D et vérifier que ABCD est bien un parallélogramme.
Touche M : Masquer les constructions.

Prototype

GéoPlan permet d'automatiser cette dernière construction avec un prototype permettant de trouver le 4^e sommet d'un parallélogramme.

À partir de trois points A, B et C, le prototype calcule le point D tel que ABCD soit un parallélogramme avec l'instruction :

D sommet parallélogramme A, B, C

Télécharger le prototype GéoPlan paralel5.g2w

Dessiner un parallélogramme à partir de deux sommets et du centre

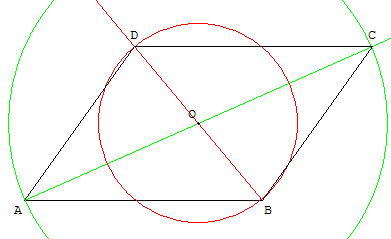Étant donné trois points A, B et O, tracer un parallélogramme ABCD tel que O que soit le point d'intersection des diagonales.

Indications : C et D sont les symétriques de A et B par rapport à O.

Il est possible de réaliser la construction, à la « règle et au compas », en traçant les diagonales [AO) et [BO) et les cercles de centre O passant par A et B.
C et D sont alors les points d'intersection des demi-droites et des cercles, convenablement choisis.

Télécharger la figure GéoPlan paralel6.g2w

Construire un parallélogramme ABCD connaissant les longueurs de deux côtés consécutifs et la longueur d'une diagonale.
Voir : problèmes de construction (à la « règle et au compas »)

Cas particuliers : Dessiner un losange

e. À partir d'un côté [AB]

Placer deux points A et B et dessiner le côté [AB],
tracer le cercle de centre A passant par B, placer le sommet D sur ce cercle et tracer segment [AD],
tracer les cercles de centres B et D passant par A, le dernier sommet D est le deuxième point d'intersection de ces cercles.
Tracer les côtés [CD] et [AD].

Il est possible de tracer les diagonales et de marquer leur angle droit.

Commandes GéoPlan
Touche M : Masquer les constructions,
touche D : afficher les Diagonales.

Télécharger la figure GéoPlan losange1.g2w
Télécharger la figure Cabri cons_losange1.fig
Télécharger la figure GeoLabo losange1.glb

f. À partir d'une diagonale [AC]

Placer deux points A et C, tracer un cercle (c) de centre A et de rayon a, supérieur à AC/2.
Tracer un cercle (c’) de même rayon et de centre C.

Les cercles (c) et (c’) se coupent en B et D. La droite (BD) est la médiatrice du segment [AC].

Tracer le quadrilatère ABCD et montrer que ABCD est un losange, marquer les égalités de côtés.
Marquer le centre O, l'angle des diagonales et remarquer les droites parallèles.

Les « anciens Égyptiens » utilisaient cette méthode, par exemple dans la construction des pyramides, pour tracer un angle droit :
prendre une corde, faire un nœud au milieu et fixer les deux extrémités sur deux piquets placés en A et C. Tendre la corde de part et d'autre de (AC) en la prenant par le nœud et marquer les points B et D, puis le centre O.

Télécharger la figure GéoPlan losange.g2w
Télécharger la figure Cabri cons_losange.fig
Télécharger la figure GeoLabo losange.glb

g. Rectangle

Dessiner le segment [AB], tracer la perpendiculaire à [AB] passant par A,
placer un point D sur la perpendiculaire (menu : créer > point > point libre >sur une droite),
tracer les parallèles à (AB) passant par C et à (BC) passant par A,
C est le point d'intersection de ces deux parallèles.

Tracer les segments [BC], [CD] et [AD].

Il est possible de dessiner les diagonales et le cercle circonscrit au rectangle.

Commandes GéoPlan
Touche M : Masquer les constructions,
touche D : afficher les Diagonales,
touche C : afficher le Cercle circonscrit et son centre O.

Télécharger la figure GéoPlan de base rectangle.g2w ; la figure GéoPlan rectangl.g2w
Télécharger la figure Cabri rectangle.fig
Télécharger la figure GeoLabo rectangle.glb

h. Carré : construction à partir d'un côté [AB]

Placer deux points libres A et B et dessiner le segment [AB],
tracer la perpendiculaire à [AB] passant par B et le cercle de centre B passant par A.
Le sommet D est un des points d'intersection de cette perpendiculaire et du cercle.
Construire les perpendiculaires à (AB) en B et à (AD) en D.
Construire le point C comme intersection de ces deux perpendiculaires.

Télécharger la figure GéoPlan carre.g2w
Télécharger la figure Cabri carre.fig
Télécharger la figure GeoLabo carre.glb

i. Carré : construction à partir d'une diagonale [AC]

Tracer deux points libres A et C, le segment [AC] et son milieu O.
La médiatrice (d) de [AC] coupe le cercle (c) de diamètre [AC] en B et D.
Tracer le losange ABCD et montrer que ABCD est un carré.

Commandes GéoPlan
Déplacer les points A, B ou D et vérifier que ABCD est bien un parallélogramme.
Touche M : Masquer les constructions,
touche D : afficher les Diagonales.

En classe de quatrième, on calculera la longueur du côté du carré avec la relation de Pythagore dans le triangle OAB :
AB = r où r est le rayon du cercle circonscrit (c₁).

Télécharger la figure GéoPlan carre2.g2w
Télécharger la figure Cabri carre2.fig
Télécharger la figure GeoLabo carre2.glb

Voir : carré au collège

Sommaire
Faire de la géométrie dynamique

2. Théorème de Varignon

Un quadrilatère étant donné, si l'on joint les milieux des côtés consécutifs, on obtient un parallélogramme.

Ce résultat est valable quel que soit le quadrilatère convexe, concave ou croisé.

En corollaire les médianes d'un quadrilatère ont même milieu (étant les diagonales du parallélogramme), leur milieu G est le centre de gravité du quadrilatère.
Le périmètre du parallélogramme de Varignon est égal à la somme des longueurs des diagonales du quadrilatère,
l'aire du quadrilatère, non croisé, est le double de celle du parallélogramme de Varignon.

Si ABCD est un quadrilatère non croisé, appliquer le théorème de Varignon aux quadrilatères (croisés) ABDC et ACBD permet d'obtenir deux autres parallélogrammes.

Pour un quadrilatère, les milieux et des côtés, les milieux des deux côtés opposés et des diagonales forment des parallélogrammes.
Ces trois parallélogrammes ont même milieu : le centre de gravité G du quadrilatère.
Les droites qui joignent les milieux des côtés et les milieux des diagonales se coupent en G qui est leur milieu.

Commandes GéoPlan
Taper M pour afficher les médianes du quadrilatère, concourantes au point G, centre de gravité.
Taper P pour obtenir les parallélogrammes joignant les milieux de deux côtés opposés et les milieux des diagonales.

Démonstration

« IJKL est un parallélogramme » peut être démontré dès la classe de quatrième, grâce au théorème des milieux des côtés d'un triangle :
on montre que les côtés opposés de IJKL sont chacun parallèle à une diagonale de ABCD, donc parallèles entre eux :
par exemple, [IL] et [JK] sont parallèles et leurs longueurs égales à la moitié de [BD].

Calcul de l'aire :
Soit ABCD quadrilatère non croisé (convexe).
Soit d = BD diagonale de ABCD, base des triangles ABD et CBD. Toujours d'après le théorème des milieux, la base b = JK du parallélogramme IJKL est égale à la moitié de d.
La hauteur h du parallélogramme, prise perpendiculairement à la diagonale (BD), se décompose en deux longueurs h₁ et h₂ de part et d'autre de la droite (BD).
h₁ est égale à la moitié de la hauteur h₁’ issue de A de ABD et h₂ est égale à la moitié de la hauteur h₂’ issue de C de CBD.

Donc, Aire(ABCD) = Aire(ABD) + Aire(CBD) = × d × h₁’ + × d × h₂’ = × d × (h₁’ + h₂’) = × 2b × (2h₁ + 2h₂) = × 2b × 2h = 2 × Aire(IJKL).

Pierre Varignon (1654-1722), ami de Jean Bernouilli, est surtout connu pour avoir assis en France les idées de Leibniz sur l'analyse (reprises par De L'Hospital) face à l'opposition de Rolle et aux travaux de Newton.

Colette Jean-Paul - Histoire des mathématiques - Éditions du renouveau pédagogique - 1973
Voir : Varignon - Marc Blanchard - Plot n^o 58 - 1992

Télécharger la figure GéoPlan varignon.g2w
Télécharger les figures Cabri varignon.fig et varignon2.fig
Télécharger les figures GeoLabo varignon.glb et varignon2.glb

3. Parallélogramme et milieux

Dans un parallélogramme, les segments, joignant deux sommets opposés aux milieux des côtés opposés, sont parallèles et partagent la diagonale joignant les deux autres sommets en trois parties égales.

ABCD est un parallélogramme de milieu O, M est le milieu de [AB] et N le milieu de [CD].

O est le milieu commun de la diagonale [BD] et de la médiane [MN].
MBND est un parallélogramme et (MD) est parallèle à (BN).

M est le milieu de [AB] donc, dans le triangle ABL, le point K est le milieu de [AL] et AK = KL,
N est le milieu de [CD] donc, dans le triangle CDK, le point L est le milieu de [KC] et KL = LC.
K et L partagent [AC] en trois segments de longueur égale.

Télécharger la figure GéoPlan parallelogramme_milieu.g2w

Voir aussi : partage d'un segment en trois : constructions élémentaires, règle à bords parallèles
Pliage d'une feuille en trois parties égales : constructions - pliages

Applications
Centre de gravité d'un triangle

Le centre de gravité d'un triangle est situé aux des médianes à partir des sommets :
À partir d'un triangle ABD, construire le point C, symétrique de A par rapport au milieu O de [BD], permet d'obtenir le parallélogramme de la figure ci-dessus. [AO] et [CM] sont deux médianes de ABD qui se coupent en K, centre de gravité du triangle.
AK = AC = AO car AO = AC. Le point K situé au tiers de [AD] est aux deux tiers de la médiane [AO].

Cas particulier

Si le parallélogramme ABCD est tel que AB = 2 AD, en remarquant que BCNM est alors un losange, montrer que :

(BN) est perpendiculaire à (MC),
IMJN est un rectangle.

Les points I et J sont les milieux des parallélogrammes AMND et MBCN.
La droite (IJ) est parallèle à (AB) et à (CD) ; [IJ] et [AC] ont même milieu O.

Télécharger la figure GéoPlan parallelogramme_milieu_rect.g2w
Télécharger la figure Cabri mul_parallelogramme_milieu.fig
Télécharger la figure GeoLabo mul_parralelogramme_milieu.glb

Rectangle

Dans un rectangle ABCD, les droites (MD) et (BN) sont perpendiculaires à la diagonale (AC), si AB = CD.

Figure incomplète

ABCD est un parallélogramme, M est le milieu de [AB] et K est situé au tiers de [MD].

Que penser du point K ? Quel segment tracer pour trouver une solution ?

Indications

Point de vue des configurations : tracer les diagonales [AC] et [BD] qui se coupent en O.
K est le centre de gravité du triangle ABD, situé aux deux tiers de la médiane [AO], donc au tiers de [AC].

Point de vue vectoriel : tracer la diagonale [AC].
Montrer que =

Cliquer dans la figure et taper S pour une solution.

Télécharger la figure GéoPlan parallelogramme_incomplet.g2w

4. Parallélogramme avec contraintes

Construire un parallélogramme dont deux sommets sont situés sur deux droites

On donne deux points A, B distincts et deux droites (d₁), (d₂) sécantes, et distinctes de (AB).

Existe-t-il un point C sur (d₂) et un point D sur (d₁) tel que le quadrilatère ABCD soit un parallélogramme ?

Analyse

Placer un point D libre sur (d₁) et construire le quatrième point C du parallélogramme ABCD.
Déplacer le point D jusqu'à ce que C soit sur la droite (d₂).

Commandes GéoPlan

Cliquer dans la figure et déplacer le point D

T : Traces du point C,
S : Sortie du mode trace,
L : afficher/cacher le Lieu géométrique de C,
P: tracer/cacher le Parallélogramme solution.

Solution

La trace du lieu du point C permet de réaliser que ce point est situé sur une droite parallèle à (d₁).

Il suffit donc de tracer la droite (d’) image de (d₁) par la translation de vecteur . Les droites (d₂) et (d’) sont sécantes en C.

Le point D, image de C par la translation réciproque de vecteur , est situé sur (d₁) et = : le parallélogramme ABCD est la solution du problème.

Télécharger la figure GéoPlan para_sur_2_droites.g2w
Sommaire
Faire de la géométrie dynamique

5. Multiplication de l'aire d'un parallélogramme

Ces deux parallélogrammes ont même milieu O.

Commandes GéoPlan

Cliquer dans la figure et :
taper sur la touche D pour afficher les diagonales,
taper P pour prolonger les côtés de ABCD.

Démonstration 1 : utilisation de parallélogrammes.

En raison de la symétrie de centre B, = ,
et pour celle de centre D, = .
Par ailleurs, ABCD est un parallélogramme donc = .
Ces trois égalités permettent d'écrire : = 2 = 2 = , APCR est un parallélogramme : les diagonales [AC] et [RP] se coupent en leur milieu : O est le milieu de [RP].

De même, on montre que dans le parallélogramme BQDS, O est le milieu de [QS].

Réciproquement : les diagonales du quadrilatère PQRS se coupent en leur milieu O, c'est un parallélogramme.

Démonstration 2 : symétrie de centre O.

Dans la symétrie de centre B, B est point fixe et P a pour image A.
Dans la symétrie de centre O, B et A ont pour images D et C.
Dans la symétrie de centre D, D est invariant et C a pour image R.

En composant ces trois symétries, nous obtenons une symétrie centrale qui transforme B en D : c'est la symétrie de centre O, dans cette symétrie P a pour image R.

De même, en composant les symétries de centres A, O et C, on montre que cette composée est la symétrie de centre O qui transforme S en Q. O est le centre de symétrie du quadrilatère PQRS : c'est un parallélogramme.

Démonstration 3 : égalité de vecteurs

Avec une relation de Chasles calculer les vecteurs et :
= + = + 2 ,
= + = 2 + .

Comme ABCD est un parallélogramme on a = et = .
Les vecteurs et sont égaux : PQRS est un parallélogramme.

Aire : les triangles CQR, DRS, ASP et BPQ ont même hauteur que le parallélogramme ABCD, relativement à des bases deux fois plus grandes, Il ont même aire que ABCD (ou bien remarquer que l'aire de CQR est la moitié de l'aire du parallélogramme CQC’R, où C’ est le symétrique de C par rapport à L. Le parallélogramme CQC’R a une aire double de celle de ABCD).
L'aire de PQRS, égale à l'aire de ABCD, augmentée des aires des quatre triangles, est égale à cinq fois l'aire du petit parallélogramme.

Réciproquement, on peut retrouver le petit parallélogramme à partir du grand, en joignant les sommets aux milieux des côtés suivants (dans le sens direct).

Télécharger la figure GéoPlan mul_parall.g2w
Télécharger la figure Cabri mul_parallelogramme.fig
Télécharger la figure GeoLabo mul_parralelogramme.glb

Carré

ABCD est un carré, P est le symétrique de A par rapport à B, Q est le symétrique de B par rapport à C, R est le symétrique de C par rapport à D et S est le symétrique de D par rapport à A. Montrer que PQRS est un carré d'aire cinq fois plus grande.

La rotation de centre O et d'angle 90° transforme [AP] en [BQ],
[BQ] en (CR)…

P a pour image Q, Q a pour image R, R a pour S et S a pour image P. Le quadrilatère PQRS globalement invariant par la rotation a ses quatre côtés de même longueur, deux côtés consécutifs forment un angle de 90°, égal à l'angle de la rotation. ADCD est un carré.

Si le côté du petit carré AB = a, la propriété de Pythagore dans le triangle BPQ permet de calculer PQ = a. PQRS a une aire égale à 5a².

Voir : pavages
Composer un carré somme de deux carrés de côtés a et b : carré au collège

Commandes GéoPlan

Cliquer dans la figure :
taper D pour effacer les diagonales,
taper P pour effacer les prolongements des côtés du petit carré.

Télécharger la figure GéoPlan mul_carres.g2w

Prolongements

Les symétries centrales sont, lorsque k = 2, un cas particulier de l'exercice plus général suivant :

Soit ABCD un parallélogramme et k un réel positif.

Sur la demi-droite [BA) on place le point P tel que AP = k BA.
Sur la demi-droite [CB) on place le point Q tel que BQ = k CB.
Sur la demi-droite [DC) on place le point R tel que CR = k DC.
Sur la demi-droite [AD) on place le point S tel que DS = k AD.

Montrer que PQRS est un parallélogramme.

Voir : le quadrilatère qui tourne

Télécharger la figure GéoPlan mul_parall_2.g2w
Télécharger la figure Cabri mul_parallelogramme_2.fig
Télécharger la figure GeoLabo mul_parralelogramme_2.glb

À la place du parallélogramme, il possible d'envisager n'importe quel polygone régulier convexe.
Voir aussi l'étude avec des triangles, dans : triangle en second