|
Géométrie dynamique avec GéoPlan : angles inscrits égaux et supplémentaires, théorème limite de cocyclicité, milieux d'arcs et bissectrices, quadrilatères inscriptibles. | ||
 Angles inscrits au collège |
| |
Sommaire1. Angles inscrits |
Angle rotationArc capable Triangle rectanglePage no 103, créée le 4/2/2007, modifiée le 26/11/2007 | ||||
|
Si vous ne visualisez pas l'image dans le cadre ci-contre, les contrôles ActiveX du CREEM ne sont pas installés sur votre PC. Vous pouvez :
| |||||
|
Exercices de géométrie | Collège | GéoPlan | GéoPlan 4e | GéoPlan | GéoPlan |
1. Angles inscrits
Classe de troisième
Soit (c) un cercle de centre O et de rayon r, A et B deux points de ce cercle et M un point libre sur le cercle (c).
|
L'angle inscrit AMB intercepte l'arc AB. AÔB est l'angle au centre correspondant.
|
Deux angles inscrits qui interceptent le même arc ont la même mesure. AMB = ANB.
|
Lorsque deux points M et N sont de part et d'autre de la corde [AB], les angles inscrits AMB et ANB sont supplémentaires : AMB + ANB = 180°
|
Corde et tangenteThéorème limite de cocyclicité L'angle inscrit BMA a même mesure que l'angle BÂT de la corde [BA] et de la tangente [AT). Démonstration : Si H est le milieu de [AB], les angles HÔA et BÂT ont leurs côtés deux à deux perpendiculaires, ils sont égaux. (OH) étant la bissectrice du triangle isocèle BOA,
|
Démonstration Cas où l'angle AMB est aigu ; A et B de part et d'autre de (MO) Soit I le deuxième point de rencontre du cercle (c) avec le diamètre issu de M. Si le point I est entre A et B faire l'addition des angles :
Arc capable : angle-rotation | |
2. Angle inscrit dans un demi-cercle : théorème dû à Thalès
Un angle inscrit dans un demi-cercle est droit.
![]() Télécharger la figure GéoPlan tr_rect5.g2w
Télécharger la figure GéoPlan tr_rect5.g2w
Sommaire
Faire de la géométrie dynamique
3. Bissectrice
Si M est un point variable sur l'arc AB, le point I, intersection de la bissectrice de l'angle inscrit AMB avec (c), est fixe : c'est le milieu de l'arc AB.
Réciproquement, si I est le milieu d'un arc AB, et M un point du cercle situé sur le complément de l'arc AB ne contenant pas I, alors la droite (MI) est la bissectrice de l'angle inscrit AMB.
Application : les points d'intersection des bissectrices d'un triangle avec son cercle circonscrit sont les milieux des arcs déterminés par les sommets.
![]() Télécharger la figure GéoPlan bissectrice.g2w
Télécharger la figure GéoPlan bissectrice.g2w
Problèmes de constructions
Constructions utilisant des configurations connues
CAPES Externe de Mathématiques - Épreuve sur dossier - sujet no 19 du 20 juillet 2006
L'exercice proposé :
Soit (Γ) un cercle de centre O et [AB] une corde de (Γ). Soit M un point de (Γ), distinct de A et de B. La bissectrice de AMB coupe (Γ) en I.
a. À l'aide d'un logiciel de géométrie dynamique, construire la figure. Quelle conjecture peut-on faire sur le point I et sur le triangle AIB lorsque M décrit un arc de cercle d'extrémités A et B ?
b. Démontrer cette conjecture et préciser la position de I.
c. Soit (Γ) un cercle de centre O, [AB] une corde de (Γ) et N un point de ]AB[. Construire un triangle ABC tel que C Î (Γ) et tel que la bissectrice de ACB passe par N.
Le travail demandé au candidat :
Q.a. Présenter la figure réalisée sur la calculatrice et l'animation permettant de mettre en évidence la conjecture.
Q.b. Dégager les propriétés mises en jeu dans la résolution de l'exercice et indiquer à quel niveau on peut le proposer.
c. Le candidat rédigera et présentera plusieurs énoncés d'exercices, variés, de constructions de triangles vérifiant des conditions métriques ou géométriques.
Indications
L'exercice proposé par le jury se situait délibérément à un niveau de troisième ou de seconde ;
il s'appuyait essentiellement sur le théorème dit de l'angle inscrit. La rédaction de la réponse à la question a. pouvait se limiter à l'observation de l'invariance du point I d'intersection lorsque l'on déplace le point M, la conjecture étant donc que ce point est fixe.
c. Le point C est le deuxième point d'intersection du cercle (Γ) et de la droite (IN).
![]() Télécharger la figure GéoPlan construc_triangle.g2w
Télécharger la figure GéoPlan construc_triangle.g2w
4. Quadrilatère inscriptible - Points cocycliques
Définitions
Des points cocycliques sont situés sur un même cercle.
Un quadrilatère est inscriptible si les quatre sommets sont cocycliques.
Un quadrilatère est inscriptible dans un cercle si (et seulement si) deux angles opposés sont égaux ou supplémentaires.
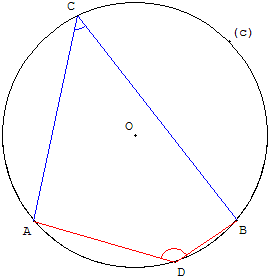
a. Quadrilatère croisé (papillon)Rappel : un quadrilatère ACBD est croisé si les deux diagonales [AB] et [CD] sont à l'extérieur du quadrilatère. Un quadrilatère croisé est concave. Un quadrilatère croisé est inscriptible si (et seulement si) deux angles opposés sont égaux. ACB = ADB. Les deux autres angles opposés sont aussi égaux.
|
b. Quadrilatère convexeRappel : un quadrilatère ACBD est convexe si les deux diagonales [AB] et[CD] sont à l'intérieur du quadrilatère.
Un quadrilatère convexe est inscriptible si (et seulement si) deux angles opposés sont supplémentaires. ACB + ADB = 180°. Les deux autres angles opposés sont aussi supplémentaires.
|
Angles orientés
Quatre points A, B, C et D sont cocycliques (ou alignés) si et seulement si on a : (![]() ,
, ![]() ) = (
) = (![]() ,
, ![]() ) (mod π).
) (mod π).
Voir : théorème de Ptolémée
Sommaire
Faire de la géométrie dynamique
c. Orthogonalité
Quatre points A, B, C et D sont placés dans cet ordre sur un cercle (Γ). Le point a est le milieu de l'arc AB, b de l'arc BC, c de l'arc CD et d de l'arc DA.
Les droites (ac) et (bd) se coupent en I. Montrer qu'elles sont perpendiculaires.
Commande GéoPlan
Cliquer dans la figure et taper S pour la solution.
Indications : étude d'angles pour montrer que le triangle Iab est rectangle.
(ab) est la bissectrice de BâC, (ac) est la bissectrice de CâD ; (ba) est la bissectrice de BbA et (bd) est la bissectrice de AbD.
L'angle bâc est égal à la moitié de BâD et l'angle abd à la moitié de BbD.
Les angles inscrits BâD et BbD sont supplémentaires, leurs moitiés sont complémentaires :
bâc + abd = 90°.
L'angle en I du triangle Iab est droit, car aIb + bâc + abd =180°.
![]() Télécharger la figure GéoPlan cocy_ortho.g2w
Télécharger la figure GéoPlan cocy_ortho.g2w
Les points J et K sont les centres des cercles inscrits dans les triangles ABD et ACD. Montrer que la droite (bd) est la médiatrice de [JK].
|
Les points L et M sont les centres des cercles inscrits dans les triangles BCD et ABC.
|
Solution
Cliquer dans la figure ci-dessus à gauche et taper S pour la solution.
Le centre J du cercle inscrit dans le triangle ABD est situé à l'intersection des bissectrices (Da) et (Bd).
Dans le cercle (Γ) l'angle ADa est la moitié de l'angle ADB. Cet angle inscrit est égal à l'angle inscrit AdB.
Dans le cercle de centre d, passant par A, et par D (sur le cercle Γ, le point d est le milieu de l'arc AD), soit J’ l'intersection de ce cercle avec [dB], l'angle au centre AdJ’ est la moitié de l'angle inscrit ADJ’. J’ est aussi sur (Da) : J et J’ sont confondus. Le point J est situé sur le cercle.
On montre, de même, que le centre K du cercle inscrit dans le triangle ACD est situé sur le cercle de centre d passant par A.
La droite (db), bissectrice de l'angle BdC, est la médiatrice de la corde [JK] (axe de symétrie du triangle isocèle dJK).
5. Trapèze isocèle
|
Deux parallèles coupent un cercle selon un trapèze.
Deux droites parallèles (d) et (d’) coupent un cercle (c) en A, B et C, D de telle façon que
ABCD soit un trapèze convexe. Montrer que ABI est un triangle isocèle. Indications Les angles inscrits BÂC et BDC sont égaux.
Sommaire |
Montrer que le trapèze est isocèle :
Deux droites parallèles (d) et (d’) coupent un cercle (c), de centre O, en formant un trapèze ABCD. Montrer que ABCD est un trapèze isocèle. Indications ABI est isocèle, d'où BÂC = ABD, O, I et J sont alignés sur la droite (HK) médiatrice de [AB] et [CD].
|
6. Milieux d'arcs et cordes
A, B et C étant trois points situés sur un cercle (c), D est le milieu de l'arc AB et E le milieu de l'arc AC.
La droite (DE) coupe la corde (AB) en F et la corde (AC) en G.
Démontrer que AF = AG.
Indications
Les arcs AD et DB sont égaux et on les égalités d'angles inscrits α = BÂD = ABD = AED.
De même, les arcs AE et EC sont égaux et β = CÂE = ECA = EDA.
Les angles externes EGC et DFB des triangles EAG et DAF sont égaux à α + β.
De même, les angles opposés par le sommet AGF = AFG = α + β.
Le triangle AGF est isocèle et AF = AG.
![]() Télécharger la figure GéoPlan mi_corde.g2w
Télécharger la figure GéoPlan mi_corde.g2w
7. Triangle inscrit dans deux cercles sécants
Deux cercles (c) et (c’) de centres distincts I et J sont sécants en A et B.
Soit C un point du cercle (c). La droite (BC) recoupe le cercle (c’) en D.
Que dire du triangle ACD lorsque l'on déplace le point C sur le cercle (c).
Indication
Le triangle ACD a des angles fixes, les mêmes angles que AIJ (Ces triangles sont semblables).
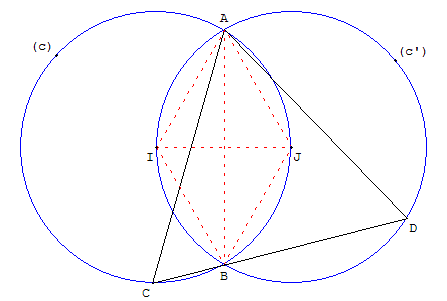
Chacun des cercles passe par le centre de l'autre
|
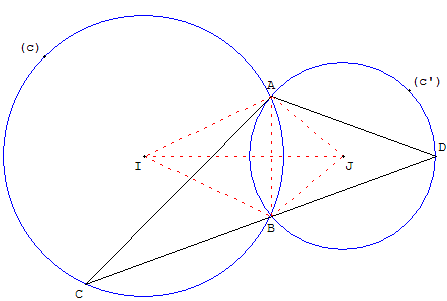
Cas général
|
Étudier les angles inscrits ACB et ADB :
– en les comparant aux angles aux centres AIB et AJB,
– ou bien en étudiant le cas particulier où [AC] est un diamètre de (c).
Cas particuliers :
le triangle ACB est équilatéral si, chacun des cercles passe par le centre de l'autre,
Il est isocèle, si les cercles sont de même rayon (seconde, voir : alignement avec un point et son transformé),
Il est rectangle, si le triangle AIJ est rectangle (les cercles sont orthogonaux).
Collège | GéoPlan | GéoPlan en 4e | GéoSpace 3e | Cabri-Géomètre | |
Sommaire1. Angles inscrits |
Faire de la géométrie dynamiqueSuggestions, remarques, problème : me contacter. | ||||